（二）人口增长模型

人口增长问题，最开始是由社会学家关注的问题。英国的经济学家和人口学家马尔萨斯(Thomas Robert Malthus)最先研究这个问题，马尔萨斯在其著作《人口原理》提出了一个基本假设。

                                                                                 

基本假设：

人口的自然增长率是一个常量，人口的变化率和当前的人口数目成正比。

基于这样的一个基本假设，我们可以建立一个可用来描述人口数量随时间演化的数学模型。设 $t$时刻 人口数量为 $x(t)$, $t+\Delta t$时刻人口的数量为 $x(t+\Delta t)$,设人口的自然增长率为 $\lambda$.依据假设

\[\frac{x(t+\Delta t)-x(t)}{x(t)\Delta t}=\lambda\]
令$\Delta t \to 0$,得到常微分方程
\[\frac{dx}{dt}=\lambda x(t)\]
我们选定一个时刻作为原点统计此时的人口数量 $x(0)=N_{0}$
上述微分方程很容易求解
\[x(t)=N_{0}e^{\lambda t}\]
长时间的渐进行为
\[\lim_{t\to +\infty}x(t)=+\infty\]
这就引起了“马尔萨斯灾难”，所谓“马尔萨斯灾难”是指人口的数量呈指数形式增长，而资源（粮食等）的增长是线性的，除了自然原因或者主动节育，人口的增长带来的灾难是不可避免的。这也是我国实行计划生育的理论依据
这个模型不仅在一定程度上回答了人口增长问题，对于类似的物种增长问题都做了回答，在短时期内与现实较好的吻合。这个模型的缺陷是显而易见的，基本假设过于简单，一个基本的事实是由于客观环境限制人口增长速率不可能趋于无穷大。

                                                               
1938年，Logistic模型提出，这个模型是马尔萨斯模型的修正模型认为$\lambda$应该是$t$的函数，并且这个函数具有这样的性质

当人口数量越接近环境总容量时，人口的自然增长率越低。

可用一个简单数学公式描述，最简单地设\[\lambda(t)=M-x(t)\]

这样我们得到了微分方程
\[\frac{dx}{dt}=(M-x(t))x(t),x(0)=N_{0}\]
当$M>>x(t)$时，近似的退化成马尔萨斯模型。对上面的模型进行求解
\[x(t)=\frac{M}{1-Ce^{-Mt}},C=1-\frac{M}{N_{0}}\]
长时间的渐进行为
\[\lim_{t\to\infty}x(t)=M\]

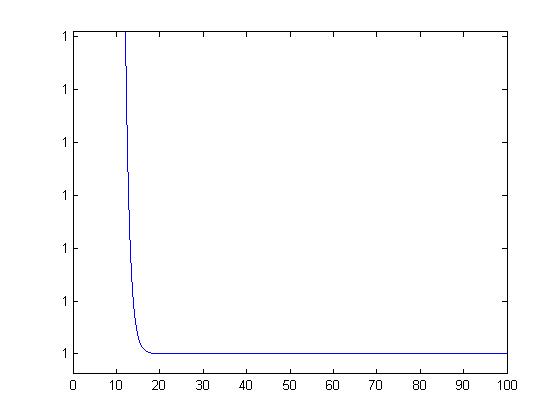
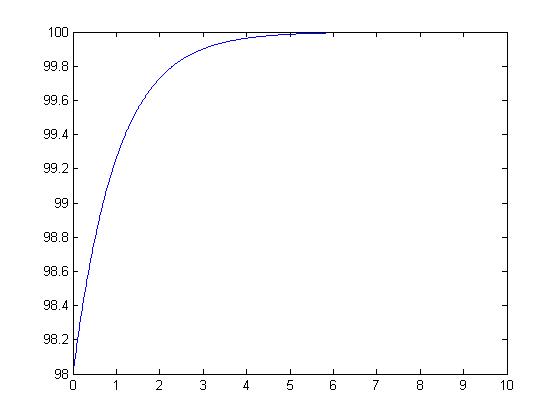
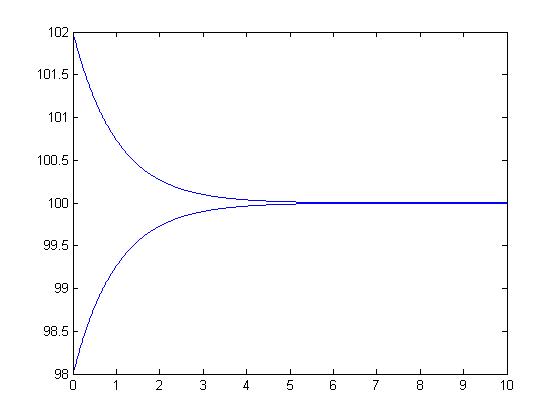
分析平衡点令 $\frac{dx}{dt}=0$，得 $x_{1}=0,x_{2}=M$.

                当$0<x<M$ 时即物种数量尚未达到环境容量上限，$dx/dt>0$ 物种数量增加直至趋于环境容量上限。

                当 $x>M$ 时物种数量已经超过环境容量上限，$dx/dt<0$ 物种数量递减直至趋于环境容量上限。

分析平衡点稳定性:

                                $\frac{d^{2}x}{dt^{2}}|_{x_{2}}=-M<0$ 是稳定的平衡点；

                                $\frac{d^{2}x}{dt^{2}}|_{x_{1}}=M>0$ 是不稳定的平衡点。

令 $\frac{d^{2}x}{dt^{2}}=0$ 得到 $x^{*}=\frac{M}{2}$ 即当物种数量达到环境容量上限的一半时，物种增长的最快。

对离散形式的Logistic映射会产生chaos现象。有文章在研究分数阶的Logistic映射，这个以后再作补充说明。

 

Remark：

1. 物种的的增长速率未必和当前的物种数量相关，可能取决于孕期的雌性物种的数量，因此可建立时滞型的微分方程模型

\[\frac{dx}{dt}=f(x(t-\tau))\]

关于时滞型微分方程的分析更加复杂，可以参看专著。

2. 若物种的增长速率和之前所有时刻都相关则建立的模型及其分析更加复杂。目前比较热门的分数阶微分方程模型即属于此类。

3. 一些参数需要统计得知，这里面又涉及到参数估计等。可以在方程里添加些噪声，分析下噪声的影响等。

转载于:https://www.cnblogs.com/zhangwenbiao/p/3708796.html