欧式距离(Euclidean distance):
两点 x=(x1, x2, x3) , y=(y1, y2, y3) 之间的欧式距离为:d(x, y) = ![]()
曼哈顿距离(Manhattan distance):
两点 x=(x1, x2, x3) , y=(y1, y2, y3) 之间的欧式距离为:d(x, y) = |x1 – y1| + |x2 – y2| + |x3 – y3|
马氏距离(Mahalanobis distance):
(1) 对于一个样本X,其均值 u=![]() ,协方差矩阵为
,协方差矩阵为 ![]() ,其马氏距离为:d =
,其马氏距离为:d =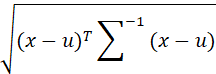
如果![]() 是单位矩阵,则马氏距离退化成欧式距离。马氏距离用来度量一个样本点到样本分布中心的距离。
是单位矩阵,则马氏距离退化成欧式距离。马氏距离用来度量一个样本点到样本分布中心的距离。
(2)当然,马氏距离也可以度量两个来自同一分布的样本x和y的相似性:
d =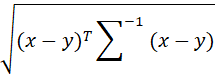




 博客介绍了Python相关内容,重点提及几种距离度量方法,包括欧式距离、曼哈顿距离和马氏距离,给出了两点间欧式距离和曼哈顿距离的计算公式,还阐述了马氏距离度量样本点到分布中心距离及两个样本相似性的情况,若协方差矩阵为单位矩阵,马氏距离退化为欧式距离。
博客介绍了Python相关内容,重点提及几种距离度量方法,包括欧式距离、曼哈顿距离和马氏距离,给出了两点间欧式距离和曼哈顿距离的计算公式,还阐述了马氏距离度量样本点到分布中心距离及两个样本相似性的情况,若协方差矩阵为单位矩阵,马氏距离退化为欧式距离。

















 5743
5743

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








