11. Container With Most Water

最大面积求解

最新推荐文章于 2024-10-29 13:54:07 发布

weixin_34037515

最新推荐文章于 2024-10-29 13:54:07 发布

阅读量54

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/skillking/p/9403791.html

本文介绍了一种求解给定纵坐标数组中所能组成的最大面积的方法。通过定义两个指针从数组两端向中间移动，每次计算当前面积并更新最大面积值。此算法适用于计算机科学中的数据结构与算法课程。

一、题目

　　1、审题：

　 2、分析：

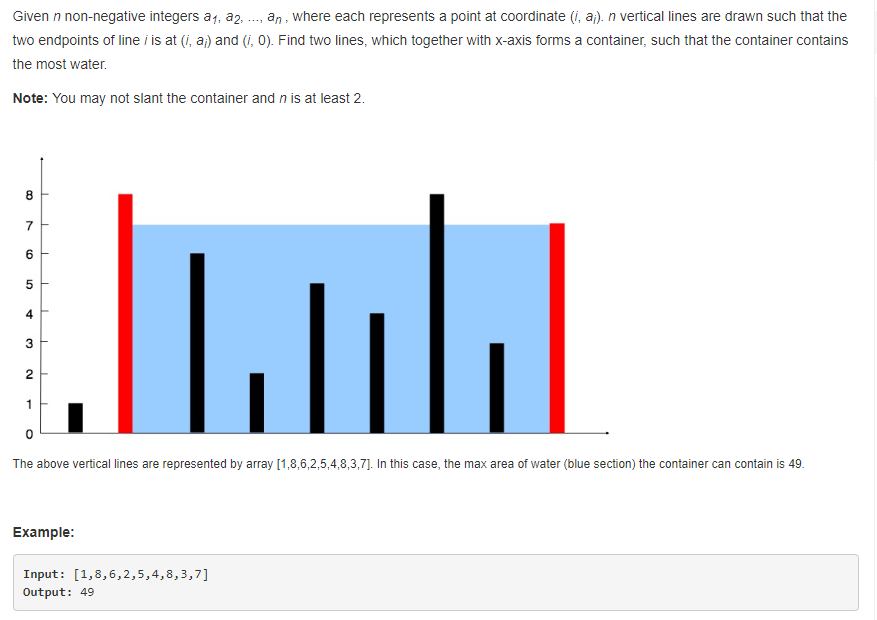
　　　　　给出纵坐标的数组，求两个坐标所能组成的最大面积。

二、解答

　　1、分析：

　　　　a、记数组下标 low=0 和 high=数组长-1；

　　　　b、low 和 high 相向而行，求得所组成最大面积；

　　　　　　其中判断条件为，若 low 所在纵坐标比 high所在纵坐标大，则 high--，否则 low++；

　　　　　　记录每一次坐标所组成的面积大小；

　　　　　　若 low >= high, 则跳出循环；

class Solution {
    public int maxArea(int[] height) {

        int maxArea = 0, tempArea = 0;
        int low = 0, high = height.length - 1;

        while(low < high) {

            tempArea = (high - low) * Math.min(height[low], height[high]);
            if(tempArea > maxArea)
                maxArea = tempArea;

            if(height[low] < height[high])
                low++;
            else
                high--;

        }

        return maxArea;
    }
}