详解基于朴素贝叶斯的情感分析及 Python 实现

相对于「 基于词典的分析 」，「 基于机器学习 」的就不需要大量标注的词典，但是需要大量标记的数据，比如：

还是下面这句话，如果它的标签是：

服务质量 - 中 （共有三个级别，好、中、差）

╮(╯-╰)╭，其是机器学习，通过大量已经标签的数据训练出一个模型，

然后你在输入一条评论，来判断标签级别

宁馨的点评 国庆活动，用62开头的信用卡可以6.2元买一个印有银联卡标记的冰淇淋，
有香草，巧克力和抹茶三种口味可选，我选的是香草口味，味道很浓郁。
另外任意消费都可以10元买两个马卡龙，个头虽不是很大，但很好吃，不是很甜的那种，不会觉得腻。
标签：服务质量 - 中

  朴素贝叶斯

1、贝叶斯定理

假设对于某个数据集，随机变量C表示样本为C类的概率，F1表示测试样本某特征出现的概率，套用基本贝叶斯公式，则如下所示：

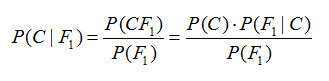
上式表示对于某个样本，特征F1出现时，该样本被分为C类的条件概率。那么如何用上式来对测试样本分类呢？

举例来说，有个测试样本，其特征F1出现了（F1=1），那么就计算P(C=0|F1=1)和P(C=1|F1=1)的概率值。前者大，则该样本被认为是0类；后者大，则分为1类。

对该公示，有几个概念需要熟知：

先验概率（Prior）。P(C)是C的先验概率，可以从已有的训练集中计算分为C类的样本占所有样本的比重得出。

证据（Evidence）。即上式P(F1)，表示对于某测试样本，特征F1出现的概率。同样可以从训练集中F1特征对应样本所占总样本的比例得出。

<