题解:当度数大于等于3的点最多只有一个时可以遍历,否则不行。一次dfs找出以那个点为根节点的所有叶子节点(配合vector遍历)
#include <map> #include <set> #include <stack> #include <cmath> #include <queue> #include <cstdio> #include <vector> #include <string> #include <cstring> #include <iostream> #include <algorithm> #define debug(a) cout << #a << " " << a << endl using namespace std; const int maxn = 1e5 + 10; const int mod = 1e9 + 7; typedef long long ll; ll n, u, v, vis[maxn]; vector<ll> V[maxn], ans; struct node { ll num, val; }deg[maxn]; bool cmp( node a, node b ) { return a.num > b.num; } void dfs( ll k, ll last ) { vis[k] = 1; if( V[k].size() == 1 && V[k][0] == last ) { ans.push_back(k); return ; } for( ll i = 0; i < V[k].size(); i ++ ) { if( !vis[V[k][i]] ) { dfs( V[k][i], k ) ; } } return ; } int main(){ std::ios::sync_with_stdio(false); cin >> n; memset( vis, 0, sizeof(vis) ); for( ll i = 1; i <= n; i ++ ) { deg[i].val = i; } for( ll i = 1; i < n; i ++ ) { cin >> u >> v; deg[u].num ++, deg[v].num ++; V[u].push_back(v), V[v].push_back(u); } sort( deg+1, deg+n+1, cmp ); if( deg[2].num >= 3 ) { cout << "No" << endl; } else { cout << "Yes" << endl; dfs( deg[1].val, -1e9 ); cout << ans.size() << endl; for( ll i = 0; i < ans.size(); i ++ ) { cout << deg[1].val << " " << ans[i] << endl; } } return 0; }




 本文介绍了一种针对树形结构(无向连通且不含环的图)的有效分解方法,旨在将树的边划分成若干简单路径,确保任意两条路径至少有一个公共顶点,每条边恰好属于一条路径。通过实例解析了算法实现过程及有效性验证。
本文介绍了一种针对树形结构(无向连通且不含环的图)的有效分解方法,旨在将树的边划分成若干简单路径,确保任意两条路径至少有一个公共顶点,每条边恰好属于一条路径。通过实例解析了算法实现过程及有效性验证。
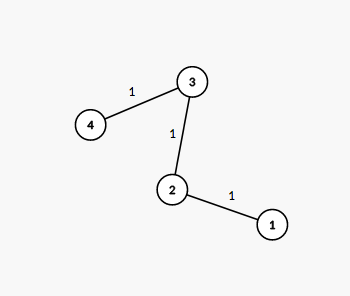 The number next to each edge corresponds to the path number in the decomposition. It is easy to see that this decomposition suits the required conditions.
The number next to each edge corresponds to the path number in the decomposition. It is easy to see that this decomposition suits the required conditions.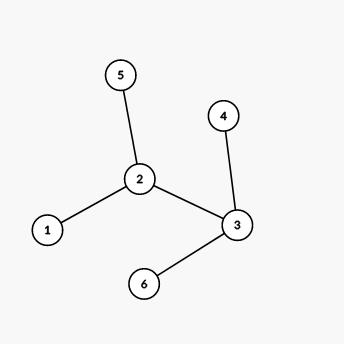 We can show that there are no valid decompositions of this tree.
We can show that there are no valid decompositions of this tree.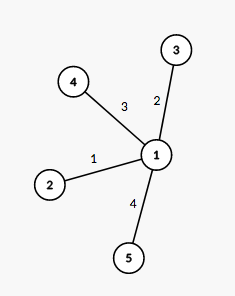 The number next to each edge corresponds to the path number in the decomposition. It is easy to see that this decomposition suits the required conditions.
The number next to each edge corresponds to the path number in the decomposition. It is easy to see that this decomposition suits the required conditions.
















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








