六 排序
这章将讨论元素的排序问题。为了简单起见,假设在我们的例子中数组只包含整数,当然更复杂的对象也是可以的。对本章的大部分内容,还要假设整个排序工作能够在主存中完成,因此,排序的元素个数相对来说比较少(少于几百万)。在磁盘上的完成的排序叫做外部排序。我们对内部排序的考查将包括:
-
存在几种容易的算法以Ο(N^2)排序,如插入算法。
-
还有一种算法叫做谢尔排序(Shellsort),它编程非常简单,以Ο(N^2)运行,并在实践中很有效。
-
还有一些稍微复杂的Ο(NlogN)的排序算法。
-
任何通用的排序算法均需要Ω(NlogN)次比较。
本章其余部分将描述和分析各种排序算法。这些算法包含一些有趣的和重要的代码优化和算法设计思想。排序还是一种能够进行精确分析的算法范例。
6.1 预备知识
我们描述的算法是可以互换的。每个算法都将接收包含一些元素的数组:假设所有的数组位置都包含要排序的数据的数据。还假设N是传递到排序方法的元素个数。
假设还存在“<”和“>”操作符,用于将输入按一致次序放置。除赋值运算外,这种运算是仅有的允许对输入数据进行的操作。在这条件下的排序称为基于比较的排序(comparison-based sorting)。这些接口与STL中的排序算法不同。STL中排序是通过使用函数模板sort来完成的。sort的参数反映了一个容器(的范围)的头尾标志,以及一个可选的比较器:
void sort( Iterator begin, Iterator end );
void sort( Iterator begin, Iterator end, Comparable cmp );迭代器必须只是随机访问的。sort算法不保证相等的项保持它们原始的次序(如果这样很重要,可以使用stable_sort来代替)。
6.2 插入排序
6.2.1 算法
插入排序(insertion sort)是由N-1趟(pass)排序组成。对于p=1到N-1趟,插入排序保证从位置0到位置p上的元素已排序状态。插入排序利用了这样的事实:位置0到位置p-1的元素是已经排过序的。图6-1显示了一个简单的数组在每一趟插入排序后的情况。
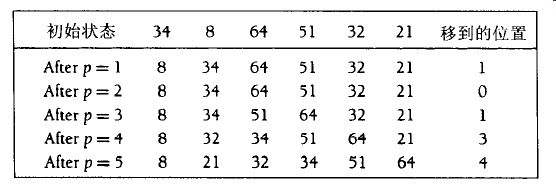
图6-1 每趟后的插入排序
图6-1表达了一般的策略。在第p趟,我们将位置p上的元素向左移动至它在前p+1个元素中的正确位置上。下面是实现的代码。
/**
* Simple insertion sort
*/
template <typename Comparable>
void insertionSort( vector<Comparable> & a )
{
int j;
for( int p = 1; p < a.size(); p++ )
{
Comparable tmp = a[ p ];
for( j = p; j > 0 && tmp < a[ j - 1 ]; j-- )
a[ j ] = a[ j - 1 ];
a[ j ] = tmp;
}
}6.2.2 插入排序的STL实现
使用STL介绍的几个观点来转换上面的算法。明显的观点是:
-
我们必须编写一个双参数排序和一个三参数排序的方法。假定双参数排序调用三参数排序,同时使用less<Object>()作为第三个参数。
-
数组访问必须转换成迭代器访问。
-
原始代码的11行需要建立tmp,在新代码中它将具有类型Object。
下面代码将Object作为另一个模板类型参数。
template<typename Iterator>
void insertionSor( const Iterator & begin, const Iterator & end )
{
if( begin != end )
insertionSortHelp( begin, end, *begin );
}
template<typename Iterator, typename Object>
void insertionSortHelp( const Iterator & begin, const Iterator & end, const Object & obj )
{
insertionSort( begin, end, less<Object>() );
}下面是三参数排序调用四参数辅助方法,该辅助方法建立一个范型类型的Object。
template<typename Iterator, typename Comparator>
void insertionSort( const Iterator & begin, const Iterator & end, Comparator lessThan )
{
if( begin != end )
insertionSort( begin, end, lessThan, *begin );
}
template<typename Iterator, typename Comparator, typename Object>
void insertionSort( const Iterator & begin, const Iterator & end,Comparator lessThan,
const Object & obj )
{
Iterator j;
for( Iterator p = begin + 1; p != end; ++p )
{
Object tmp = *p;
for( j = p; j != begin && lessThan( tmp, *( j - 1 ) ); --j )
*j = *( j - 1 );
}
}6.2.3 插入排序的分析
由于每个嵌套循环花费N次迭代,因此插入排序为Ο(N^2),而且这个界是精确的,因为以反序的输入可以达到该界。
6.3 一些简单排序算法的下界
以数为成员的数组的逆序(inversion)是指具有性质i<j但a[i]>a[j]的序偶(i,j)。在上节的例子中,输入数据34,8,64,51,32,21有9个逆序,即(34,8)、(34,21)、(64,51)、(64,32)、(64,21)、(51,32)、(51,21)以及(32,21)。这正好是需要由插入排序(隐含)执行的交换次数。可以通过计算排序中的平均逆序数而得出插入排序平均运行时间的精确的界。
定理6.1 N个互异元素的数组的平均逆序数是N(N-1)/4。
定理6.2 通过交换相邻元素进行排序的任何算法平均需要Ω(N^2)次交换。
6.4 谢尔排序
谢尔排序(shellsort)的名字源于它的发明者Donald Shell,该算法是冲破二次时间屏障的第一批算法之一,不过,直到它最初被发现的若干年后才证明了它的亚二次性时间界。它通过比较相距一定间隔的元素来工作:各趟比较所用的距离随着算法的进行而减小,直到比较相临元素的最后一趟排序为止。由于这个原因,谢尔排序有时也叫作缩减增量排序(diminishing increment sort)。
谢尔排序使用一个序列h1,h2,…,hi,叫做增量序列(increment sequence)。只要h1=1,任何增量序列都使可行的,不过,有些增量序列比另外一些增量序列更好。在使用增量hk的一趟排序之后,对于每一个i我们有a[i]≤a[i+hk};所有相隔hk的元素都被排序。此时称文件是hk排序的(hk-sorted)。如下图所示:

图6-2 谢尔排序每趟之后的情况
hk排序的一般做法是,对于hk,hk+1,…,N-1中的每一个位置i,把其上的元素放到i,i-hk,i-2hk,…中间的正确位置。
谢尔排序的最坏情形分析
虽然谢尔排序编程简单,但其运行时间分析则完全是另一回事。它的运行时间依赖于增量序列的选择。下面是使用谢尔增量的谢尔排序。
/**
* Shellsort, using Shell's (poor) increments.
*/
template<typename Comparable>
void shellsort( vector<Comparable> & a )
{
for( int gap = a.size() / 2; gap > 0; gap /= 2 )
for( int i = gap; i < a.size(); i++ )
{
Comparable tmo = a[ i ];
int j = i;
for( ; j >= gap && tmp < a[ j - gap ]; j -= gap )
a[ j ] = a[ j - gap ];
a[ j ] = tmp;
}
}定理6.3 使用谢尔增量时谢尔排序的最坏情形运行时间为Θ(N^2)。
定理6.4 使用Hibdard增量的谢尔排序的最坏情形运行时间为Θ(N^(3/2))。
谢尔排序是算法非常简单且又具有极其复杂的分析的一个好例子。性能在实践中完全可以接收。
6.5 堆排序
堆排序(heapsort)是基于优先队列可以用于以Ο(NlogN)时间进行排序的思想。建立一个N个元素的二叉堆需要花费Ο(N)时间,然后执行deleteMin操作花费为每次Ο(logN)时间。因此总的运行时间是Ο(NlogN)。
该算法的主要问题在于,它使用了一个附加数组。因此,存储需求量增加一倍。避免使用第二个数组的聪明方法是利用这样的事实:在每次deleteMin之后,堆缩小了1。因此,堆中最后的单元可以用来存放刚刚删去的元素。
在实现中我们用max堆。第一步以线性时间建立堆,然后通过将堆中的最后元素与第一个元素交换,缩减堆的大小并进行下滤,来执行N-1次deleteMax操作。例如考虑输入序列31,41,59,26,53,58,97。最后得到的堆如图6-3所示。图6-4显示了第一次deleteMax操作之后的堆。
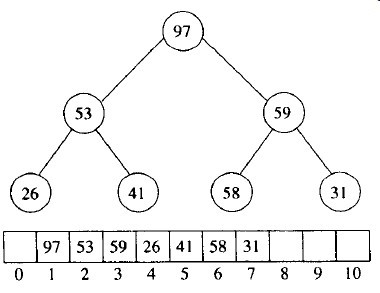
图6-3 在buildheap阶段以后的max堆
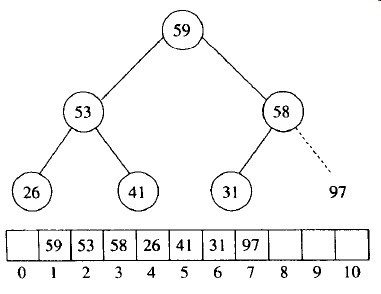
图6-4 在第一次deleteMax后的堆
堆排序的代码实现如下,稍微优点复杂的是,不像二叉堆,二叉堆的数据是从数组下标1处开始,而此处堆包含位置0处的数据。
/**
* Standard heapsort
*/
template <typename Comparable>
void heapsort( vector<Comparable> & a )
{
for( int i = a.size() / 2; i >= 0; i-- ) //buildHeap
percDown( a, i, a.size() );
for( int j = a.size() - 1; j > 0; j-- )
{
swap( a[ 0 ], a[ j ] ); //deleteMax
percDown( a, 0, j );
}
}
/**
* Internal method for heapsort.
* i is the index of an item in the heap.
* Return the index of the left child.
*/
inline int leftChild( int i )
{
return 2 * i + 1;
}
/**
* Internal method for heapsort that is used in deleteMax and buildHeap.
* i is the position from which to percolate down.
* n is the logical size of the binary heap.
*/
template <typename Comparable>
void percDown( vector<Comparable> & a, int i, int n )
{
int child;
Comparable tmp;
for( tmp = a[ i ]; leftChild[ i ] < n; i = child )
{
child = leftChild( i );
if( child != n - 1 && a[ child ] < a[ child + 1 ] )
child++;
if( tmp < a[ child ] )
a[ i ] = a[ child ];
else
break;
}
a[ i ] = tmp;
}
堆排序的分析
堆排序最坏情况下最多2NlogN-Ο(N)次比较(设N≥2)。而且是一个非常稳定的算法:它的平均使用的比较只比最坏情形指出的略少。
定理6.5 对N个互异项的随机堆列进行堆排序,所用的平均次数为2NlogN-Ο(NloglogN)。
6.6 归并排序
归并排序(mergesort)以Ο(NlogN)最坏情形运行时间运行,而所用的比较次数几乎是最优的。它是递归算法的一个很好的实例。
这个算法的基本操作是合并两个已排序的表。因为这两个表已排序,所以若将输出放到第3个表中则该算法可以通过对输入数据一趟排序来完成。基本合并算法是取两个输入数组A和B、一个输出数组C以及3个计数器(Actr、Bctr和Cctr),它们初始置于对应数组的开始端。合并例子见下。

如果数组A含1、13、24、26,数组B含有2、15、27、38,那么该算法如下进行:首先,比较1和2,1被添加到C中,然后12和2比较。

2被添加到C中,然后13和15进行比较。

13被添加到C中,接下来比较24和15,这样一直到26和27进行比较。
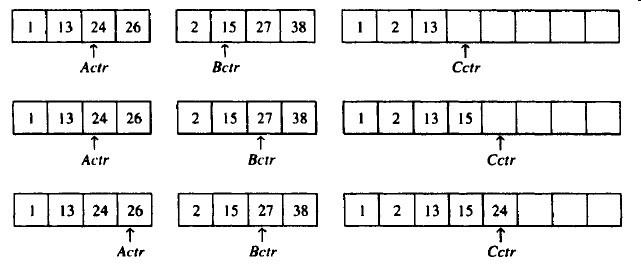
26被添加到C中,数组A已经用完。

将数组B的其余部分复制到C中。

合并两个已排序的表的时间显然是线性的,因为最多进行N-1次比较,其中N是元素的总数。
归并排序算法递归地将前半部分数据和后半部分数据各自归并排序。该算法是经典的分治(divide-and-conquer)策略,它将问题分(divide)成一些小的问题然后递归求解,而治(conquering)的阶段则是将分的阶段解得的各结果修补到一起。
下面是归并算法的一种实现。单参数mergeSort是四参数递归函数mergeSort的一个驱动程序。
/**
* Mergesort algorithm (driver)
*/
template <typename Comparable>
void mergeSort( vector<Comparable> & a )
{
vector<Comparable> tmpArray( a.size() );
mergeSort( a, tmpArray, 0, a.size() - 1 );
}
/**
* Internal method that makes recursive calls.
* a is an array of Comparable items.
* tmpArray is an array to place the merged result.
* left is the left-most index of the subarray.
* right is the right-most index of the subarray.
*/
template <typename Comparable>
void mergeSort( vector<Comparable> & a , vector<Comparable> & tmpArray, int left, int right )
{
if( left < right )
{
int center = ( left + right ) / 2;
mergeSort( a, tmpArray, left, center );
mergeSort( a, tmpArray, center + 1, right );
merge( a, tmpArray, left, center + 1, right );
}
}下面是merge方法的实现。
/**
* Internal method that merges two sorted halves of a subarray.
* a is an array of Comparable items.
* temArray is an array to place the subarray.
* leftPos is the left-most index of the subarray.
* rightPos is the index of the start of the second half.
* rightEnd is the right-most index of the subarray.
*/
template <typename Comparable>
void mergeSort( vector<Comparable> & a , vector<Comparable> & tmpArray, int leftPos,
int rightPos, int rightEnd )
{
int leftEnd = rightPos - 1;
int tmpPos = leftPos;
int numElements = rightEnd - leftPos + 1;
// Main loop
while( leftPos <= leftEnd && rightPos <= rightEnd )
if( a[ leftPos ] <= a[ rightPos ] )
tmpArray[ tmpPos++ ] = a[ leftPos++ ];
else
tmpArray[ tmpPos++ ] = a[ rightPos++ ];
while( leftPos <= leftEnd ) // Copy rest of first half
tmpArray[ tmpPos++ ] = a[ leftPos++ ];
while( rightPos <= rightEnd ) // Copy rest of right half
tmpArray[ tmpPos++ ] = a[ rightPos++ ];
// Copy temArray back
for( int i = 0; i < numElements; i++, rightEnd-- )
a[ rightEnd ] = tmpArray[ rightEnd ];
}归并排序的分析
归并排序是用于分析递归方法技巧的经典实例:必须给运行时间写一个递归关系。假设N是2的幂,从而总可以将它分裂成相等的两部分。对于N=1,归并排序所用时间是常数,我们将其记为1。否则,对N个数归并排序的用时等于完成两个大小为N/2的递归排序所用的时间再加上合并的时间,它是线性的。下述方程给出了准确描述:
T(1)=1
T(N)=2T(N/2)+N
最后得到结果:T(N)=NlogN+N-Ο(NlogN)。
虽然归并排序的运行时间是Ο(NlogN),但是它很难用于主存排序,主要问题在于合并两排序的表需要线性附加内存,在整个算法中还要花费将数据复制到临时数组再复制回来这样一些附加的工作,其结果严重减慢了排序的速度。
6.7 快速排序
顾名思义,快速排序(quicksort)是在实践中最快的已知排序算法,它的平均运行时间是Ο(NlogN)。该算法之所以快,主要是由于非常精炼和高度优化的内部循环。它最坏的性能是Ο(N^2)。通过将堆排序和快速排序结合起来,就可以在堆排序的Ο(NlogN)最坏运行时间下,得到对几乎所有输入的最快运行时间。
像递归一样,快速排序也是一种分治的递归算法。将数组S排序的基本算法由下列简单的四步组成:
-
如果S中的元素是0或1,则返回。
-
取S中任一元素v,称之为枢纽元(pivot)。
-
将S-{v}(S中其余元素)划分成两个不相交的集合:S1={x∈S-{v}|x≤v}和S2={x∈S-{v}|x≥v}。
-
返回{quicksort(S1)},后跟v,继而quicksort(S2)}。
图6-5解释了如何快速排序一个数集。
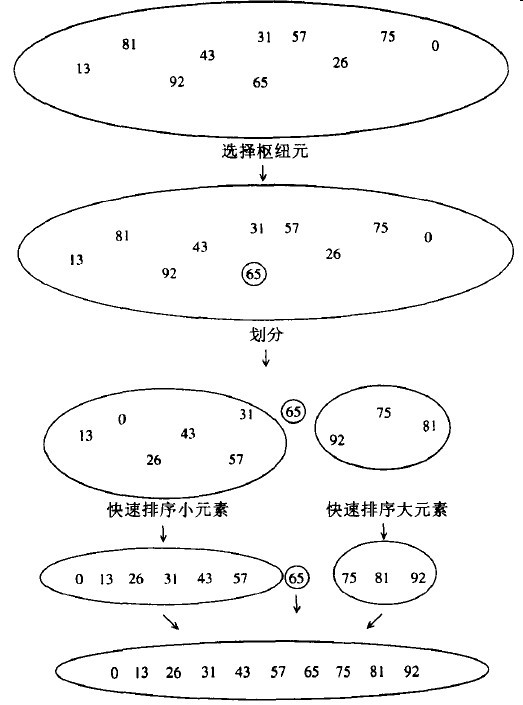
6-5 说明快速排序各步的演示示例
快速排序更快的原因在于,第三步划分成两组实际上在是在适当的位置进行并且非常有效,它的高效不仅弥补了大小不等的递归调用的补足而且还超过了它。
6.7.1 选择枢纽元
6.7.1.1 一种错误的方法
通常的、没有经过充分考虑的选择是将第一个元素用作枢纽元。如果输入是随机的,那么这是可以接收的,但如果输入是预排序或反序的,这样的枢纽元将把所有元素分入S1或S2。另一种想法是选取前两个互异的键中的较大者作为枢纽元,但这和只选取第一个元素作为枢纽元具有相同的害处。
6.7.1.2 一种安全的做法
一种安全的方针是随机选取枢纽元。一般来说这种策略非常安全,除非随机数生成器有问题。另一方面,随机数的生成一般是昂贵的,根本减少不了算法其余部分的平均时间。
6.7.1.3 三数中值分割法
一组N个数的中值是第 [N/2] 个最大的数。枢纽元的最好选择是数组中的中值。但这难算出,并且会明显减慢快速排序的速度。一般的做法是使用左端、右端和中心位置上的三个元素的中值作为枢纽元。







 本文深入探讨了排序算法的基础知识,包括插入排序、谢尔排序和堆排序的原理、实现及性能分析。通过具体代码示例和数学推导,详细解释了每种算法的工作机制、复杂度以及在实际应用中的表现。
本文深入探讨了排序算法的基础知识,包括插入排序、谢尔排序和堆排序的原理、实现及性能分析。通过具体代码示例和数学推导,详细解释了每种算法的工作机制、复杂度以及在实际应用中的表现。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








