回溯法（3）

四、0-1背包问题

问题表述：给定n种物品和一背包。物品i的重量是wi，其价值为pi，背包的容量为C。问应如何选择装入背包的物品，使得装入背包中物品的总价值最大?

0-1背包问题是一个特殊的整数规划问题。

解空间：

可行性约束函数：

上界函数：

考虑一个右子树的时候，设

r：是当前未考虑的剩余物品的总价值(remainder)

cp：是当前的价值(current price)

bestp：是当前得到的最优价值(best price)

那么，满足：

但是，上界r太松。

一个更加紧的上界：

将剩余物品按照单位重量价值排序，然后依次装入物品，直到装不下，再将剩余物品的一部分放入背包。(r_n  <=  r)

实现

/* 主题：0-1背包问题
* 作者：chinazhangjie
* 邮箱：chinajiezhang@gmail.com
* 开发语言：C++
* 开发环境：Mircosoft Virsual Studio 2008
* 时间: 2010.10.25
*/
#include <iostream>
#include <vector>
#include <algorithm>
#include <functional>
using namespace std;

class goods {
public:
	int weight; // 重量
	int price;	// 价格
	goods() : weight(0),price(0) 
	{}
};

bool goods_greater(const goods& lhs,const goods& rhs)
{
	return (lhs.price / lhs.weight) > (rhs.price / rhs.weight);
}

class knapsack 
{
public:
	knapsack (int c,const vector<goods>& gl) 
		: capacity (c), curr_price(0), best_price (0), curr_weight(0){
		goods_list = gl;
		total_layers = gl.size();
		curr_path.resize (total_layers);
		best_path.resize (total_layers);
	}
	void backtrack () {
		__backtrack (0);
		cout << "path: " ;
		copy (best_path.begin(),best_path.end(),ostream_iterator<int> (cout, " "));
		cout << endl;
		cout << "best_price: " << best_price << endl;
	}

private:
	// 计算上界
	int __bound (int layers) {
		int cleft = capacity - curr_weight;
		int result = curr_price;
		// 将layer之后的物品进行按单位价格降序排序
		vector<goods> tmp = goods_list;
		sort (tmp.begin() + layers, tmp.end(),goods_greater);
		// 以物品单位重量价值递减序装入物品
		while (layers < total_layers && tmp[layers].weight <= cleft) {
			cleft -= tmp[layers].weight;
			result += tmp[layers].price;
			++ layers;
		}
		// 装满背包
		if (layers < total_layers) {
			result += (tmp[layers].price / tmp[layers].weight) * cleft;
		}
		return result;
	}

	void __backtrack (int layers) {
		// 到达叶子结点，更新最优价值
		if (layers >= total_layers) {
			if (curr_price > best_price || best_price == 0) {
				best_price = curr_price;
				copy (curr_path.begin(), curr_path.end(), best_path.begin());
			}
			return ;
		}
		// 左剪枝（能放的下）
		if (curr_weight + goods_list[layers].weight <= capacity) {
			curr_path[layers] = 1;
			curr_weight += goods_list[layers].weight;
			curr_price += goods_list[layers].price;
			__backtrack (layers + 1);
			curr_weight -= goods_list[layers].weight;
			curr_price -= goods_list[layers].price;
		}
		// 右剪枝
		if (__bound (layers + 1) > best_price || best_price == 0 ) {
			curr_path[layers] = 0;
			__backtrack (layers + 1);
		}
		/*curr_path[layers] = 0;
		__backtrack (layers + 1);*/
	}

private:
	vector<goods> goods_list;	// 货物信息列表
	int capacity;				// 背包承载量
	int curr_price;				// 当前价格
	int curr_weight;			　　　　// 当前重量
	int best_price;				// 当前得到的最优价值
	int total_layers;			// 总层数
	vector<int> curr_path;		// 当前路径
	vector<int> best_path;		// 最优价值下的路径
};

int main() 
{
	const int size = 3;
	vector<goods> gl(size);
	gl[0].weight = 10;
	gl[0].price = 1;
	gl[1].weight = 8;
	gl[1].price = 4;
	gl[2].weight = 5;
	gl[2].price = 5;

	knapsack ks(16, gl);
	ks.backtrack ();
	return 0;
}

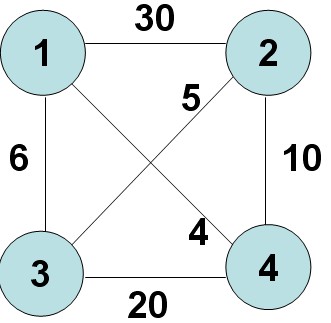
五、旅行售货员问题

问题表述：在图中找到一个权最小的周游路线

解空间：排列树

剪枝策略：

当前路径的权重＋下一个路径的权重 < 当前的最小权重，则搜索该路径

实现：

/* 主题：旅行售货员问题
* 作者：chinazhangjie
* 邮箱：chinajiezhang@gmail.com
* 开发语言：C++
* 开发环境：Mircosoft Virsual Studio 2008
* 时间: 2010.10.26
*/

#include <iostream>
#include <vector>
#include <iterator>
#include <algorithm>
using namespace std;

class traveling 
{
public:
	static const int NOEDGE  = -1 ; 
public:
	traveling (const vector<vector<int> >& ug)
		: curr_cost (0), best_cost (-1) {
		node_count = ug.size ();
		undigraph = ug;
		curr_solution.resize (node_count);
		for (int i = 0; i < node_count; ++ i) {
			curr_solution[i] = i;
		}
		best_solution.resize (node_count);
	}
	void backtrack () {
		__backtrack (1);
		cout << best_cost << endl;
	}

private:
	void __backtrack (int layers) {
		if (layers >= node_count) {
			if (undigraph[curr_solution[node_count - 1]][curr_solution[0]] == NOEDGE){
				return ;
			}
			int total_cost = curr_cost +
				undigraph[curr_solution[node_count - 1]][curr_solution[0]] ;
			if (total_cost < best_cost || best_cost == -1) {
				// 更新最优费用和最优路径
				best_cost = total_cost;
				copy (curr_solution.begin(), 
					curr_solution.end(), 
					best_solution.begin());
			}
			return ;
		}
		for (int i = layers; i < node_count; ++ i) {
			// 剪枝
			if (undigraph[curr_solution[layers - 1]][curr_solution[i]] != NOEDGE && 
				( curr_cost + undigraph[curr_solution[layers - 1]][curr_solution[i]]
				< best_cost || best_cost == -1 )) {
				// 搜索子树
				swap (curr_solution[layers],curr_solution[i]);
				curr_cost += 
					undigraph[curr_solution[layers - 1]][curr_solution[layers]];
				__backtrack (layers + 1);
				curr_cost -= 
					undigraph[curr_solution[layers - 1]][curr_solution[layers]];
				swap (curr_solution[layers],curr_solution[i]);	

			}
			
		}
	}
	int				node_count;		// 结点个数
	int				curr_cost;		// 当前费用
	int				best_cost;		// 当前
	vector<int>		curr_solution;	// 当前解决方案
	vector<int>		best_solution;	// 最优解决方案
	vector<vector<int> > undigraph; // 无向图(采用矩阵存储)
};
int main() 
{
	int size = 4;
	vector<vector<int> > ug(size);
	for (int i = 0;i < size; ++ i) {
		ug[i].resize (size);
	}

	ug[0][0] = -1;
	ug[0][1] = 30;
	ug[0][2] = 6;
	ug[0][3] = 4;

	ug[1][0] = 30;
	ug[1][1] = -1;
	ug[1][2] = 5;
	ug[1][3] = 10;

	ug[2][0] = 6;
	ug[2][1] = 5;
	ug[2][2] = -1;
	ug[2][3] = 20;

	ug[3][0] = 4;
	ug[3][1] = 10;
	ug[3][2] = 20;
	ug[3][3] = -1;

	traveling t(ug);
	t.backtrack();

	return 0;
}

 

参考书籍　《算法设计与分析（第二版）》　王晓东　编著

授课教师　张阳教授

转载于:https://www.cnblogs.com/chinazhangjie/archive/2010/10/26/1861841.html