图算法的总结

概览

• 最短路径
  • 单源最短路径
    • Dijkstra
    • Bellman-Ford
    • SPFA
  • 所有结点对
    • Floyd
• 最小生成树
  • Kruskal
  • Prim
• 拓扑排序
• 关键路径

---

【拓扑排序】

有向无环图（Directed Acyclic Graph，DAG）：有向图的任意一个顶点都不能通过一些边回到自身。

拓扑排序是将DAG图的所有结点排成一个线性序列，使得图中任意一个有向边(u->v)。在排序后，u一定在v的前面。（其实就是一个做事情的顺序，比如穿衣服，总是先穿内衣再穿外套的，即(内衣->外套)，这个顺序是不能反的。）拓扑排序后的序列又称拓扑序列。

拓扑序列的第一个顶点必然是没有前驱的，也就是它的发生不依赖其他事件的发生，即该结点的入度为0。如果有多个入度为0的点，它们之间的顺序是任意的（当有多个入度为0的点时，若要求选择结点编号最小的一个，就用priority_queue）。我们可以开一个int型数组inDegree[N]，inDegree[v]表示结点v的入度，该数组初始化为0并在数据输入的时候更新完毕。

(1).开一个队列q（queue或priority_queue），初始时把所有入度为0的结点push进队列；

(2).只要队列非空，就取出队首元素并访问它的所有邻接结点，并把所有邻接结点的入度减1，注意判断若此时某个节点的入度变为了0，就要入队；

(3).当队列为空时，如果入队元素恰好等于结点个数n，说明拓扑排序成功；否则，拓扑失败，说明图中有环。

 

拓扑排序一个很重要的应用就是判断给定的图是否是有向无环图。

下面给出一个有向图，n个结点m条边，结点编号为1~n，判断其是否为有向无环图，若是，输出其拓扑序列（若同时存在多个结点入度为0，选择结点编号最小的那个）。

代码：（数据来源 1146 Topological Order）

#include <cstdio>
#include <vector>
#include <queue>
using namespace std;
const int maxn=100;
vector<int> adj[maxn];
int inDegree[maxn]={0};
vector<int> topoSeq;
int n,m;//结点数，边数

bool topoSort()
{
    //greater 让较小的数优先级较大
    priority_queue<int,vector<int>,greater<int>> q;
    //priority_queue<int> q;
    //首先，让入度为0的点入队列
    for(int v=1;v<=n;v++)
        if(inDegree[v]==0) q.push(v);
    int cnt=0;//记录入队的结点个数
    while(!q.empty()){
        int u=q.top();
        topoSeq.push_back(u);
        q.pop();
        for(int i=0;i<adj[u].size();i++){
            int v=adj[u][i];
            inDegree[v]--;
            if(inDegree[v]==0) q.push(v);
        }
        cnt++;
    }
    if(cnt==n) return true;
    else return false;
}

int main()
{
    //freopen("pat.txt","r",stdin);
    scanf("%d%d",&n,&m);
    int u,v;
    for(int i=0;i<m;i++){
        scanf("%d%d",&u,&v);
        adj[u].push_back(v);
        inDegree[v]++;
    }
    bool flag=topoSort();
    if(flag) {
        printf("Yes\n");
        for(auto it:topoSeq) printf("%d ",it);
    }else{
        printf("No\n");
    }
    return 0;
}

 

【关键路径】

AOE网（Activity On Edge）是指用边表示活动，点表示事件的有向图，其中边权表示完成活动所需要的时间。实际上AOE网就是有向无环图（DAG）.

AOE网是基于工程提出来的，它用来解决两个问题：

1. 某工程从起始到结束至少需要多少时间？
2. 哪条（or哪些）路径上的活动是影响整个工程进度的关键？

这里需要厘清的概念是：

关键路径其实就是AOE网的最长路径，其长度等于该工程的最短完成时间。

AOE网中的最长路径被称为关键路径，而关键路径上的活动被称为关键活动。由于AOE网实际就是有向无环图（DAG），求关键路径就是在DAG图中求解最长路径。

 

以下图为例进行讲解：

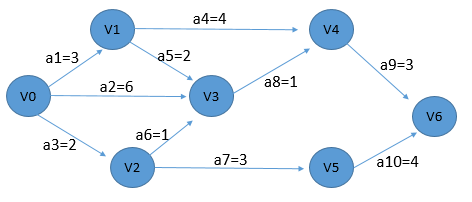
事件Vi的最早发生时间ve(i)和最晚发生时间vl(i)（ve=vertex early，vl=vertex late）

计算Vi的最早发生时间ve(i)是从V0->V1->...->V6的顺序进行的，即源点到汇点。假设结点V_j有V_i1，Vi_2，V_i3，...，V_ip这p个前驱结点，那么ve(j) = max{ ve(ik)+length(V_ik, V_j) }，其中k从1至p。由顺序拓扑序列求解得到。

计算Vi的最晚发生时间vl(i)是从V6->V5->...->V0的顺序进行的，即汇点到源点。假设结点V_j有V_i1，Vi_2，V_i3，...，V_ip这p个后继结点，那么vl(j) = min{ vl(ik) - length(V_j, V_ik ) }，其中k从1至p。由逆序拓扑序列求解得到。

顶点	V0	V1	V2	V3	V4	V5	V6
ve(i)	0	3	2	6	7	5	10
vl(i)	0	3	3	6	7	6	10

活动ai的最早开始时间e(i)和最晚开始时间l(i)。假设活动ak在Vi->Vj之间，则有：

最早开始时间e(k) = ve(i)

最晚开始时间l(k) = vl(j) - length(Vi, Vj)

若e(k) == l(k)，说明活动k是关键活动，因为最晚开始时间等于最早开始时间，即这个活动不能拖延，否则会拖延整个工程！

活动	a1	a2	a3	a4	a5	a6	a7	a8	a9	a10
e(i)	0	0	0	3	3	2	2	6	7	5
l(i)	0	0	1	3	4	5	3	6	7	6

关键路径如下图：

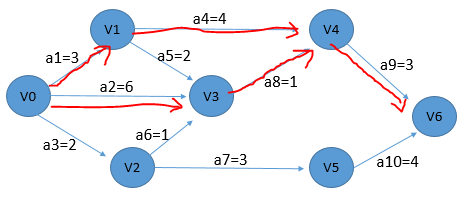
问题：

给出有向图的顶点数N，边数M，以及起点S和终点E，求出关键路径的长度和所有关键活动，并打印所有关键路径。

样例输入：

7 10 0 6

0 1 3

0 2 2

0 3 6

1 4 4

1 3 2

2 3 1

2 5 3

3 4 1

4 6 3

5 6 4

代码：

#include <cstdio>
#include <queue>
#include <stack>
#include <vector>
#include <algorithm>
using namespace std;
const int N=100;
struct Node{
    int v;//邻边结点
    int w;//权重 
    Node(int v_,int w_):v(v_),w(w_){} 
};
vector<Node> Adj[N];
int ve[N],vl[N];//结点的最早开始时间和最晚开始时间
int inDegree[N]={0};
vector<int> pre[N];//pre[u]记录结点u的前驱 
stack<int> reversedTopoSeq;//逆拓扑序列 
int n,m,s,e;//结点数，边数，起点，终点 

//求逆拓扑序列，并计算ve[N] 
bool topoSort()
{
    fill(ve,ve+N,0);//初始化各个结点的最早开始时间 
    priority_queue<int,vector<int>,greater<int>> q;
    for(int v=0;v<n;v++)
        if(inDegree[v]==0) q.push(v);
    while(!q.empty()){
        int u=q.top();
        q.pop();
        reversedTopoSeq.push(u);
        for(auto node:Adj[u]){//u->v
            int v=node.v, w=node.w;
            inDegree[v]--;
            if(inDegree[v]==0) q.push(v);
            if(ve[u]+w > ve[v]) ve[v]=ve[u]+w;//update
        }
    } 
    return (reversedTopoSeq.size()==n ? true : false);    
} 

//获取关键路径 
void getCriticalPath()
{
    //首先，根据逆拓扑序列求出vl[]
    fill(vl,vl+N,ve[n-1]);
    while(!reversedTopoSeq.empty()){
        int u=reversedTopoSeq.top();
        reversedTopoSeq.pop();
        for(auto node:Adj[u]){//u->v
            int v=node.v, w=node.w;
            if(vl[v]-w < vl[u]) vl[u]=vl[v]-w;
        }
    } 
    
    //计算活动a(k)的最早开始时间a_early和最晚开始时间a_late
    //假设活动a(k)介于vi->vj之间 
    for(int u=0;u<n;u++){
        for(auto node:Adj[u]){//u->v
            int v=node.v, w=node.w;
            int a_early=ve[u];
            int a_late=vl[v]-w;
            if(a_early==a_late) {
                printf("(%d->%d)\n",u,v);
                pre[v].push_back(u);
            }    
        }
    }
}

//打印路径 
vector<int> path; 
void dfs(int v)
{    
    path.push_back(v);
    if(v==s){
        for(auto it=path.rbegin();it!=path.rend();it++)
            printf("%d ",*it);
        printf("\n");
        return;
    }
    for(auto next:pre[v]){
        dfs(next);
        path.pop_back();
    }
}

int main() 
{
    //freopen("pat.txt","r",stdin);
    scanf("%d%d%d%d",&n,&m,&s,&e);
    int u,v,w;
    for(int i=0;i<m;i++){
        scanf("%d%d%d",&u,&v,&w);//有向边(u->v),权重w 
        Adj[u].push_back(Node(v,w));
        inDegree[v]++;
    }    
    bool flag=topoSort();
    if(flag){
        printf("Yes\n");
        printf("critical path length:%d\n",ve[n-1]);//关键路径的长度，即工程完工的最短时间 
        getCriticalPath();//获取路径 
        dfs(e);//打印路径 
    }else{
        printf("Sorry\n");
    }
    return 0;
}

 

 

 

 

转载于:https://www.cnblogs.com/kkmjy/p/9568239.html