2019届宝鸡文数质检Ⅲ解析版

前言

选择题

例7【2019届宝鸡文数质检Ⅲ第7题】双曲线\(\cfrac{x^2}{36}-\cfrac{y^2}{9}=1\)的一条弦被点\(P(4，2)\)平分，那么这条弦所在的直线方程为【】

$A.x-y-2=0$ $B.2x+y-10=0$ $C.x-2y=0$ $D.x+2y-8=0$

分析：使用点差法求解，设弦的两个端点\(A(x_1，y_1)\)，\(B(x_2，y_2)\)，则由于两个点都在双曲线上，

故满足\(\cfrac{x_1^2}{36}-\cfrac{y_1^2}{9}=1\)①，且\(\cfrac{x_2^2}{36}-\cfrac{y_2^2}{9}=1\)②，

两式做差得到，\(\cfrac{x_1^2-x_2^2}{36}-\cfrac{y_1^2-y_2^2}{9}=0\)，变形得到\(\cfrac{y_2-y_1}{x_2-x_1}\cdot \cfrac{y_2+y_1}{x_2+x_1}=\cfrac{1}{4}\)

又由于\(\cfrac{y_1+y_2}{2}=2\)，\(\cfrac{x_1+x_2}{2}=4\)，代入上式得到\(k\cdot \cfrac{2}{8}=\cfrac{1}{4}\)，故\(k=\cfrac{1}{2}\)，

由于弦过点\(P(4，2)\)，且斜率为\(k=\cfrac{1}{2}\)，求得直线为\(x-2y=0\)，故选\(C\).

例8【2019届宝鸡文数质检Ⅲ第8题】甲、乙两名同学分别从“动漫”、“武术”、“摄影”三个社团中随机选取一个社团加入，则这两名同学加入同一个社团的概率是【】

$A.\cfrac{1}{4}$ $B.\cfrac{1}{3}$ $C.\cfrac{1}{2}$ $D.\cfrac{2}{3}$

分析：两个同学分别从三个社团中任选一个加入，共有9种等可能的结果，其他加入同一个社团的情形有3种，故所求概率为\(P=\cfrac{3}{9}=\cfrac{1}{3}\)，选\(B\)。

引申：这两名同学加入了不同社团的概率是\(1-\cfrac{1}{3}=\cfrac{2}{3}\)；

例9【2019届宝鸡文数质检Ⅲ第9题】一个算法的程序框图如图所示，若该程序输出\(\cfrac{25}{42}\)，则判断框中应该填入的条件是【】

$A.i\leq 4$ $B.i\leq 5$ $C.i\leq 6$ $D.i\ge 5$

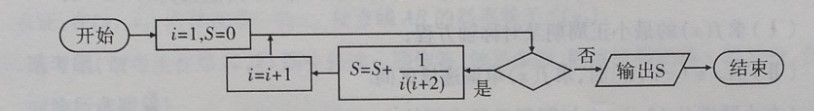
分析：按照框图的思路执行以下几个步骤，

\(R_1\)中，\(i=1，S=0\)，是，\(S=\cfrac{1}{2}(1-\cfrac{1}{3})\)，\(i=2\)；

\(R_2\)中，\(i=2，S=\cfrac{1}{2}(1-\cfrac{1}{3})\)，是，\(S=\cfrac{1}{2}(1-\cfrac{1}{3}+\cfrac{1}{2}-\cfrac{1}{4})\)，\(i=3\)；

\(R_3\)中，\(i=3，S=\cfrac{1}{2}(1-\cfrac{1}{3}+\cfrac{1}{2}-\cfrac{1}{4})\)，是，\(S=\cfrac{1}{2}(1-\cfrac{1}{3}+\cfrac{1}{2}-\cfrac{1}{4}+\cfrac{1}{3}-\cfrac{1}{5})\)，\(i=4\)；

\(R_4\)中，\(i=4，S=\cfrac{1}{2}(1+\cfrac{1}{2}-\cfrac{1}{4}-\cfrac{1}{5})\)，是，\(S=\cfrac{1}{2}(1+\cfrac{1}{2}-\cfrac{1}{4}-\cfrac{1}{5}+\cfrac{1}{4}-\cfrac{1}{6})\)，\(i=5\)；

\(R_5\)中，\(i=5，S=\cfrac{1}{2}(1+\cfrac{1}{2}-\cfrac{1}{5}-\cfrac{1}{6})\)，是，\(S=\cfrac{1}{2}(1+\cfrac{1}{2}-\cfrac{1}{5}-\cfrac{1}{6}+\cfrac{1}{5}-\cfrac{1}{7})=\cfrac{1}{2}(1+\cfrac{1}{2}-\cfrac{1}{6}-\cfrac{1}{7})=\cfrac{25}{42}\)，\(i=6\)；

\(R_6\)中，\(i=6，S=\cfrac{25}{42}\)，否，输出\(S=\cfrac{25}{42}\)，结束；即当\(i=6\)时，应该满足“否”而不是“是”，故应该填入的是\(i\leq 5\)。

例10【2019届宝鸡文数质检Ⅲ第10题】已知\(M\)，\(N\)是椭圆\(\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1\) \((a>b>0)\)上关于原点对称的两个点，\(P\)是椭圆上任意一点，直线\(PM\)，\(PN\)的斜率分别是\(k_1\)、\(k_2\)，若\(|k_1k_2|=\cfrac{1}{4}\)，则椭圆的离心率为【】

$A.\cfrac{1}{2}$ $B.\cfrac{\sqrt{2}}{2}$ $C.\cfrac{\sqrt{3}}{2}$ $D.\cfrac{\sqrt{2}}{3}$

分析：采用特殊化策略求解，由于点\(M\)，\(N\)是椭圆\(\cfrac{x^2}{a^2}+\cfrac{y^2}{b^2}=1\) \((a>b>0)\)上关于原点对称的任意的两个点，那么就可以特殊化为椭圆的左右两个顶点，又点\(P\)是椭圆上任意一点，那么就可以特殊化为椭圆上的上顶点，

那么如何让他们满足题目的条件呢，我们可以这样想，只要调整椭圆的三个参数恰当，就可以让其满足题目的条件，这样在这种特殊条件下，

\(k_1=k_{PM}=\cfrac{y_2-y_1}{x_2-x_1}=\cfrac{b-0}{0+a}\)，\(k_2=k_{PN}=\cfrac{b-0}{0-a}\)，

则\(|k_1k_2|=|\cfrac{b^2}{-a^2}|=\cfrac{b^2}{a^2}=\cfrac{1}{4}\)，故\(a^2=4b^2\)，\(c^2=a^2-b^2=3b^2\)，

则\(e^2=\cfrac{c^2}{a^2}=\cfrac{3b^2}{4b^2}=\cfrac{3}{4}\)，故\(e=\cfrac{c}{a}=\cfrac{\sqrt{3}}{2}\)。故选\(C\)。

例11【2019届宝鸡文数质检Ⅲ第11题】定义在\(R\)上的函数\(y=f(x)\)满足以下三个条件：

①对于任意的\(x\in R\)，都有\(f(x+1)=f(x-1)\)；

②函数\(y=f(x+1)\)的图像关于\(y\)轴对称；

③对于任意的\(x_1，x_2\in [0，1]\)，都有\([f(x_1)-f(x_2)](x_1-x_2)>0\)；

则\(f(\cfrac{3}{2})\)、\(f(2)\)、\(f(3)\)的大小关系是【】

$A.f(\cfrac{3}{2})>f(2)>f(3)$ $B.f(3)>f(2)>f(\cfrac{3}{2})$ $C.f(\cfrac{3}{2})>f(3)>f(2)$ $D.f(3)>f(\cfrac{3}{2})>f(2)$

分析：本题目考查函数的各种性质的综合运用，其中主要涉及的是函数的奇偶性、周期性、对称性、单调性；

由①可知，函数的周期为\(T=2\)，故可以简化其中的两项，\(f(2)=f(0)\)，\(f(3)=f(1)\)；

由②，通过图像的平移，可知函数\(y=f(x)\)的对称轴为直线\(x=1\)，即函数满足条件\(f(x)=f(2-x)\)，再赋值得到，\(f(\cfrac{3}{2})=f(2-\cfrac{3}{2})=f(\cfrac{1}{2})\)；

由③可知函数\(f(x)\)在区间\([0，1]\)上单调递增，由于\(1>\cfrac{1}{2}>0\)，故\(f(1)>f(\cfrac{1}{2})>f(0)\)，即满足\(f(3)>f(\cfrac{3}{2})>f(2)\)，故选\(D\)。

例12【2019届宝鸡文数质检Ⅲ第12题】异面直线\(a\)，\(b\)所成的角为\(\cfrac{\pi}{6}\)，直线\(a\perp c\)，则异面直线\(b\)和\(c\)所成角的范围是【】

$A.[\cfrac{\pi}{3}，\cfrac{\pi}{2}]$ $B.[\cfrac{\pi}{6}，\cfrac{\pi}{2}]$ $C.[\cfrac{\pi}{3}，\cfrac{2\pi}{3}]$ $D.[\cfrac{\pi}{6}，\cfrac{5\pi}{6}]$

分析：由于求异面直线所成角的范围，故需要先明确其允许的最大范围，是\((0，\cfrac{\pi}{2}]\)，怎么理解呢？采用简单原则，当同一平面内的两条直线相交时形成两对对顶角，其中的邻角互补，这样我们刻画其位置关系时，仅仅只需要\([0，\cfrac{\pi}{2}]\)范围内的角就足够了，不需要范围为\([0，\pi]\)，那么异面直线所成角的范围就成了\((0，\cfrac{\pi}{2}]\)，

再者我们需要将已知的直线安放在空间，最好的依托就是正方体和长方体等模型，如下图所示，

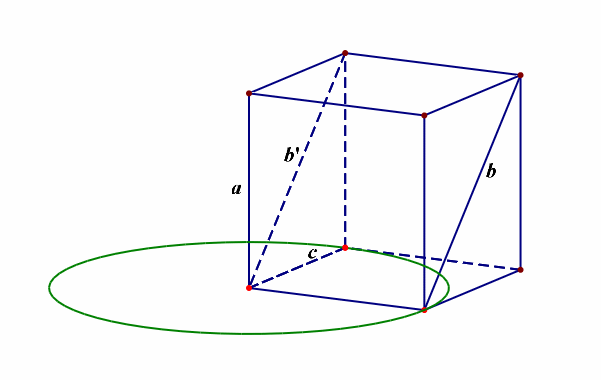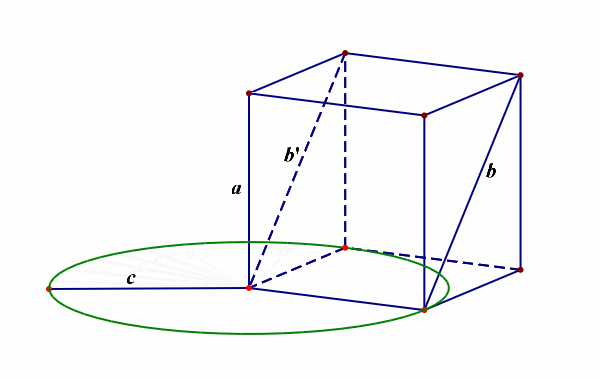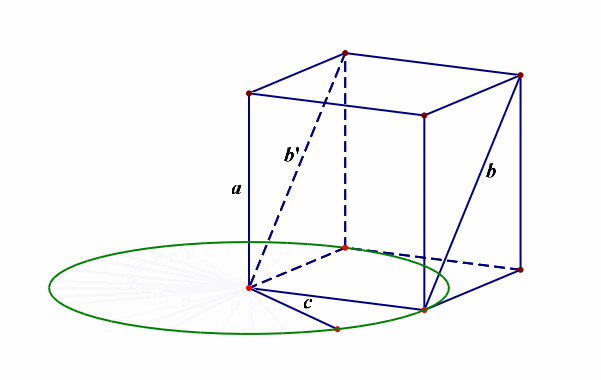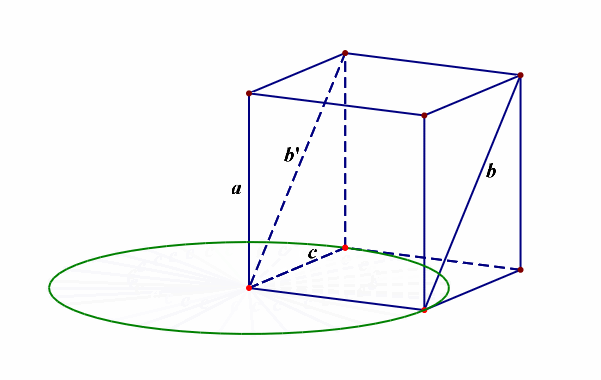
当异面直线\(a\)，\(b\)所成的角为\(\cfrac{\pi}{6}\)，直线\(a\perp c\)，那么异面直线\(b\)和\(c\)所成角的范围最小是\(\cfrac{\pi}{2}-\cfrac{\pi}{6}=\cfrac{\pi}{3}\)，最大是\(\cfrac{\pi}{2}+\cfrac{\pi}{6}=\cfrac{2\pi}{3}\)，又由于刻画异面直线所成角的范围限制，故只能是\([\cfrac{\pi}{3}，\cfrac{\pi}{2}]\)，故选\(A\)。

填空题

例13【2019届宝鸡文数质检Ⅲ第13题】若数列\(a_1+2a_2+2^2a_3+\cdots+2^{n-1}a_n=8n\) \((n\in N^*)\)，则\(a_n\)=__________。

分析：本题目的左端涉及两个数列，一个数列为\(\{a_n\}\)，设其前\(n\)项和为\(T_n\)，另一个数列为\(\{2^{n-1}a_n\}\)，设其前\(n\)项和为\(S_n\)，右端可以看出\(f(n)\)，故本题目是利用\(2^{n-1}a_n\)和\(S_n\)的关系，先求出数列\(\{2^{n-1}a_n\}\)的通项公式，然后反解出\(a_n\)即可；

由\(n\ge 1\)时，\(S_n=a_1+2a_2+2^2a_3+\cdots+2^{n-1}a_n=8n\)① ，

则\(n\ge 2\)时，\(S_{n-1}=a_1+2a_2+2^2a_3+\cdots+2^{n-2}a_{n-1}=8(n-1)\)② ，

两式做差，得到，

当\(n\ge 2\)时，\(S_n-S_{n-1}=2^{n-1}a_n=8\)，即\(a_n=8\cdot 2^{1-n}=2^{4-n}\)，

当\(n=1\)时，\(S_1=a_1=8=2^{4-1}\)，满足上式，

故\(a_n=2^{4-n}(n\in N^*)\)；

例14【2019届宝鸡文数质检Ⅲ第14题】

分析：设\(f(x)=ax^2+bx\)，则\(f'(x)=2ax+b\)，由题可知，\(f'(x)=3x-\cfrac{1}{2}\)，故\(2a=3\)，\(b=-\cfrac{1}{2}\)，故\(f(x)=\cfrac{3}{2}x^2-\cfrac{1}{2}x\)；

例15【2019届宝鸡文数质检Ⅲ第15题】

例16【2019届宝鸡文数质检Ⅲ第16题】斐波那契数列\(\{a_n\}\)：前两个数都是1，从第三个数开始，每一个数都等于它前面两个数的和，若\(b_n=a_na_{n+2}-a_{n+1}^2\)，则\(b_1+b_2+b_3+\cdots+b_{2019}\)=____________。

分析：由于斐波那契数列\(\{a_n\}\)的\(a_1=1\)，\(a_2=1\)，\(a_3=2\)，\(a_4=3\)，\(a_5=5\)，\(a_6=8\)，\(a_7=13\)，\(a_8=21\)，\(\cdots\)，

则\(b_1=a_1a_3-a_2^2=1\)；\(b_2=a_2a_4-a_3^2=-1\)；\(b_3=a_3a_5-a_4^2=1\)；\(b_4=a_4a_6-a_5^2=-1\)；\(\cdots\)，

故数列\(\{b_n\}\)为\(T=2\)的周期数列，\(b_1+b_2+b_3+\cdots+b_{2019}=1009(b_1+b_2)+b_1=1\)。

解答题

转载于:https://www.cnblogs.com/wanghai0666/p/10744697.html