HDU 6134 Battlestation Operational | 2017 Multi-University Training Contest 8

转载于 2017-08-18 16:54:00 发布 · 106 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/nicetomeetu/p/7390638.html

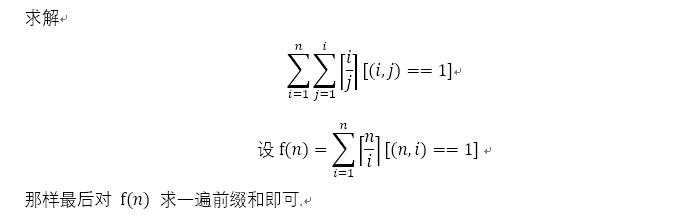
破结论没听说过，上式推导到第三步的时候有了O(nlogn) 的做法(枚举倍数+1最后前缀和)，并且这种做法可以直接应用到向上取整的计算中，详见forever97

但由于d(n)是积性函数，故可O(n)求

代码参考这里

#include <bits/stdc++.h>
using namespace std;
#define LL long long
const int N = 1e6+5;
const LL MOD = 1e9+7;
LL f[N], g[N];
void init()
{
    for (int i = 1; i < N; i++)
        for (int j = i; j < N; j += i)
            g[j] += 1;
    for (int i = 1; i < N; i++) g[i] = (g[i] + g[i-1]) % MOD;
    for (int i = 1; i < N; i++) f[i] = (g[i-1] + i) % MOD;
    for (int i = 1; i < N; i++)
        for (int j = i+i; j < N; j += i)
            f[j] = (f[j] + MOD - f[i]) % MOD;
    for (int i = 1; i < N; i++) f[i] = (f[i] + f[i-1]) % MOD;
}
int main()
{
    init(); int n;
    while (~scanf("%d", &n))
    {
        printf("%lld\n", f[n]);
    }
}

转载于:https://www.cnblogs.com/nicetomeetu/p/7390638.html