我们团队的思路也是同学在课堂上提出的动态规划问题。这样就是时空复杂度O(n)。
1.首先把数组的开始值附在一个最优解上。我们用的是,数组array3.
2.当array3[i-1]小于0时,maxsize就为他本身。
3.当array3[i-1]大于0时,maxsize就为array3[i-1]+maxsize;
#include<iostream> using namespace std; #define N 100 int shuzu(int h,int array2[N]) { int i; int array3[N]; array3[0]=array2[0]; int maxsize=array3[0]; for(i=1;i<=h;i++) { if(array3[i-1]>0) { array3[i]=array3[i-1]+array2[i]; maxsize=max(maxsize,array3[i-1]); } else { array3[i]=array2[i]; } } cout<<"子数组最大为:"<<maxsize; return 0; } int main() { int i,j; cout<<"请输入数组大小:(1-10)"<<endl; cin>>j; int array1[N]; cout<<"请输入"<<j<<"个数:"<<endl; for(i=0;i<j;i++) { cin>>array1[i]; } shuzu(j,array1); return 0; }
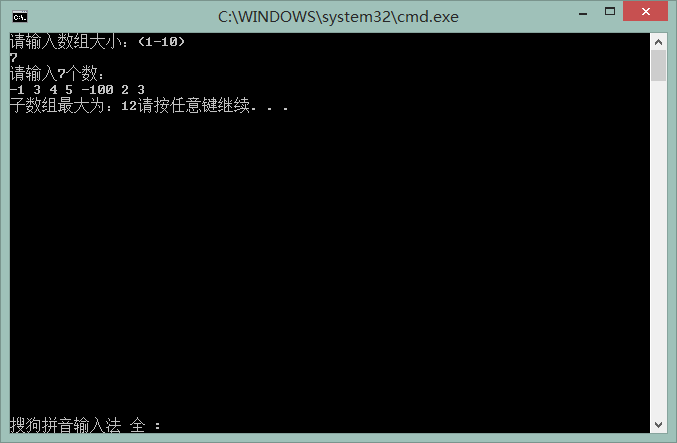




 本文介绍了一个使用动态规划解决子数组最大和问题的算法实现,通过一个示例程序详细展示了如何根据输入数组计算出子数组的最大和,并给出了完整的C++代码实现。
本文介绍了一个使用动态规划解决子数组最大和问题的算法实现,通过一个示例程序详细展示了如何根据输入数组计算出子数组的最大和,并给出了完整的C++代码实现。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








