好长时间了,继续算法导论。
当输入规模足够大时,并不计算精确的运行时间,倍增常量和低阶项被舍去。我们要研究的是算法的渐近效率,即在输入规模无限量时,在极限中,算法的运行时间如何随着输入规模的变大而增加。通常,渐近的更有效的某个算法除对很小得到输入外都是最好的选择。
3.1渐近符号
用渐近符号来刻画算法的运行时间。
这一节每有什么可写的,看书就好了。区分几个渐近符号就好。课后题是当做一下。
3.2标准记号与常用函数
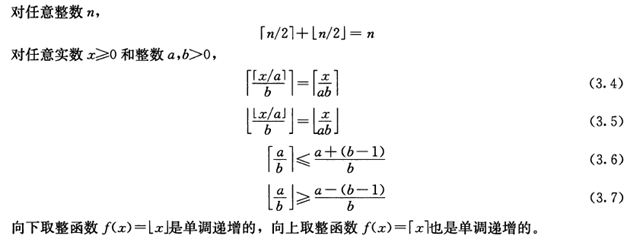
取整函数
上面的增长快慢要熟记,参考第一章的思考题1-1:http://www.cnblogs.com/batteryhp/p/4654860.html,标明了增长的快慢。
上面对e的估计比较平凡。
阶乘这一段真是长见识了。斯特林近似公式记住。
多重对数函数:
斐波那契数列
本章的课后题挑着证明一下即可。





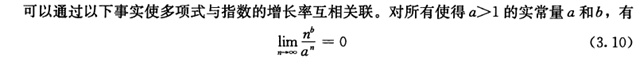



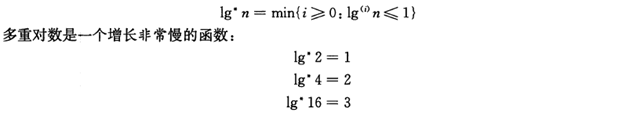



















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








