Lucas定理

最新推荐文章于 2025-02-27 21:56:34 发布

weixin_33918114

最新推荐文章于 2025-02-27 21:56:34 发布

阅读量59

点赞数

本文探讨了非负整数m和n以及素数p之间的同余关系。具体地，文中给出了m和n关于素数p展开时所遵循的一种特殊同余性质。

For non-negative integers m and n and a prime p, the following congruence relation holds:

$\binom{m}{n}\equiv\prod_{i=0}^k\binom{m_i}{n_i}\pmod p,$

where

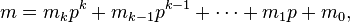
$m=m_kp^k+m_{k-1}p^{k-1}+\cdots +m_1p+m_0,$

and

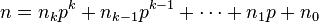
$n=n_kp^k+n_{k-1}p^{k-1}+\cdots +n_1p+n_0$

are the base p expansions of m and n respectively.

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。