AVL树-查找-插入

1. 简述

    AVL树要求每个结点的左右子树高度相差绝对值小于2。查找、插入和删除在平均和最坏情况下都是O（log n）。

2. 查找

    查找比较简单与普通二叉搜索树的查找是一样的。从根开始，要么向左，要么向右，要么找到，如果到达了NULL，则表示查找失败。   

AVLNode *  avl_search(AVLNode *  node,  int  value) {
   while (node  !=  NULL) {
     if (value  <  node -> value)  //  向左 
      node  =  node -> left;
     else   if (value  >  node -> value)  //  向右 
      node  =  node -> right;
     else   //  找到 
       return  node;
  }
   return  NULL;  //  失败 
}

3. 插入

    插入元素可能导致从根到被插入结点的这条路径的平衡会被打破，如果平衡被打破，高度差超过了1，那么需要旋转。基本流程是首先在合适位置插入结点，然后从插入位置沿着路径倒回去，逐个更新平衡度并且对需要旋转的进行合适的选择。
    旋转分四类：设当前结点为A，插入结点为C
    RR型：A的平衡度为-2，C->value > A->value并且C->value > A->right->value。C在A的右孩子的右子树中，需要一次左旋。
    LL型：A的平衡度为2，C->value < A->value并且C->value < A->left->value。C在A的左孩子的左子树中，需要一次右旋。
    RL型：A的平衡度为-2，C->value > A->value并且C->value<A->left->value。C在A的右孩子的左子树中，需要先进行一次右旋，转化为LL型，再进行一次左旋。
　 LR型：A的平衡度为2，Ｃ->value  < A->value并且C->value>A->right->value。C在A的左孩子的右子树中，需要先进行一次左旋，转化为RR型，再进行一次右旋。
    注：LL，LR这些符号，在百度百科和维基百科中的含义不一致，本文与维基百科是一致的，因为感觉维基百科的解释直观理解更清楚。LL表明C与A的位置关系是左左，LR表明C与A的位置关系时左右。
    对于双旋以前一直记不住，其实很好记，对于RR型需要左旋；对于LL型需要右旋；对于RL型，先解决后面的L，右旋，然后解决R，左旋；对于LR型，先解决后面的R，左旋，然后解决前面的L右旋。
    关于代码，网上很多都是递归的代码，我看了几篇博客文章，没发现简洁且正确的，旋转一般都没问题，但是一般旋转之后，所谓的A结点就不再是这个子树的根了，因此需要让A的父结点指向新的根，有的代码实现没有考虑到这个情况，有的代码实现虽然考虑到了这个情况，但是没有在递归的过程中，没有注意如果A的结点为空的情况，即A是根节点，根节点变了，而根是没有父结点的，此时要更新根指针。
    这里我尝试给出一个非递归的实现，不保证正确，如有错误，希望指出。   

#include < iostream >
#include < stack >
using   namespace  std;

struct  AVLNode {
  AVLNode *  left;
  AVLNode *  right;
   int  height;
   int  value;
}; 

//  更新某个结点的高度，对于多个结点分别更新，需要从叶子向根的方向调用
//  否则可能出现更新错误 
void  update_height(AVLNode  * node) {
  assert(NULL  !=  node);
   int  lheight  =  node -> left == NULL  ?   0 :(node -> left -> height + 1 );
   int  rheight  =  node -> right == NULL  ?   0 :(node -> right -> height + 1 );
  node -> height  =  lheight  >  rheight  ?  lheight : rheight;
}

//  左左情况右旋，返回子树旋转后的根 
AVLNode *  LL(AVLNode *  A) { 
  assert(NULL  !=  A);
  AVLNode *  B  =  A -> left;
  A -> left  =  B -> right;
  B -> right  =  A;
  update_height(A);
  update_height(B);
   return  B;
}
//  右右情况左旋，返回子树旋转后的根 
AVLNode *  RR(AVLNode *  A) {
  assert(NULL  !=  A);
  AVLNode *  B  =  A -> right;
  A -> right  =  B -> left;
  B -> left  =  A;
  update_height(A);
  update_height(B);
   return  B;
}
//  左右情况，先左旋后右旋，返回子树旋转后的根
AVLNode *  LR(AVLNode *  A) {
  assert(NULL  !=  A);
  A -> left  =  RR(A -> left);  //  左旋并更新A的父结点指针
   return  LL(A);  
}
//  右左情况，先右旋后左旋，返回子树旋转后的根
AVLNode *  RL(AVLNode *  A) {
  assert(NULL  !=  A);
  A -> right  =  LL(A -> right);
   return  RR(A);
}

bool  avl_insert(AVLNode *&  root,  int  value) {
  stack < AVLNode *>  store;
  AVLNode *  node, * A, * B, * C,  * tmp;
  tmp  =  root;
   //  寻找插入位置，并且保证路径 
   while (tmp  !=  NULL) {
    store.push(tmp);
     if (value  <  tmp -> value) 
      tmp  =  tmp -> left;
     else   if (value  >  tmp -> value)
      tmp  =  tmp -> right;
     else   //  插入识别 
       return   false ;
  }
   //  建立新结点
  node  =   new  AVLNode;
  node -> left  =  node -> right  =  NULL; 
  node -> height  =   0 ;
  node -> value  =  value;
   //  插入新结点 
   if (store.empty()) {  //  根结点为空 
    root  =  node;
     return   true ;
  }
   else  {
    tmp  =  store.top();
    node -> value < tmp -> value  ?  (tmp -> left = node):(tmp -> right = node);
  }
   //  对打破平衡的结点进行旋转，并且更新所有需要改变高度的结点高度 
  C  =  node;
   while ( ! store.empty()) {
    A  =  store.top();
    store.pop();
     int  lheight  =  A -> left == NULL  ?   0 :(A -> left -> height + 1 );
     int  rheight  =  A -> right == NULL  ?   0 :(A -> right -> height + 1 );
     switch (lheight - rheight) {
       case   - 1 :
       case   1 :
       case   0 :
        A -> height  =  lheight  >  rheight  ?  lheight : rheight;
         break ;
       case   2 :  //  L
         //  旋转 
         if (C -> value  <  A -> left -> value)  //  LL
          A  =  LL(A);        
         else   //  LR
          A  =  LR(A);
         //  更新父结点 
         if (store.empty())
          root  =  A;
         else  
          A -> value  <  store.top() -> value  ?  store.top() -> left  =  A : store.top() -> right  =  A;
         break ;
       case   - 2 :  //  R
         //  旋转 
         if (C -> value  >  A -> right -> value)  //  RR
          A  =  RR(A);        
         else   //  RL
          A  =  RL(A);        
         //  更新父结点
         if (store.empty())
          root  =  A;
         else  
          A -> value  <  store.top() -> value  ?  store.top() -> left  =  A : store.top() -> right  =  A;
         break ;
    }
  }
}

void  print_father_child(AVLNode *  root) {
  stack < AVLNode *>  store;
  store.push(root);
   while ( ! store.empty()) {
    root  =  store.top();
    store.pop();    
    cout  <<  root -> value  <<   "  :  " ;
     if (root -> left == NULL)
      cout  <<   " NULL " ;
     else  
      cout  <<  root -> left -> value;
    cout  <<   "  ,  " ;
     if (root -> right == NULL)
      cout  <<   " NULL " ;
     else  
      cout  <<  root -> right -> value;
    cout  <<  endl;
     if (root -> right)
      store.push(root -> right);
     if (root -> left)
      store.push(root -> left);
  }
}

int  main() {
  AVLNode *  root  =  NULL;
   for ( int  i = 0 ; i < 10 ; i ++ )
    avl_insert(root, i);
  print_father_child(root);
  system( " PAUSE " );
   return   0 ;
}

   输出结果如下： 
  

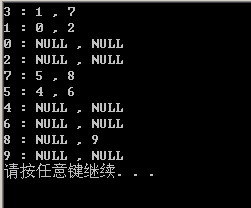
4. 删除

    写插入写了半天，删除懒得写了，就先这样的，思路是按照二叉排序树删除的方法先删除该结点，并且用栈记录从该结点到根的路径上所有结点，然后从下往上依次更新高度、检查是否平衡，对于需要旋转的情况进行旋转。
    注意更新父结点的指向以及没有父结点的情况，还有就是对于既有左孩子又有右孩子的结点，普通二叉排序树会将待删除结点交换到左子树的最右结点（或者右子树的最左结点），因此入栈记录路径时，需要分情况对待。
    代码基本上大致是普通二叉排序树的删除代码，然后加上更新检查路径的代码。

5. 参考

    维基百科_AVL树    http://zh.wikipedia.org/wiki/AVL%E6%A0%91
    百度百科_AVL树    http://baike.baidu.com/view/671745.html?tp=6_01