--Party 2
Rechard Luo
一、XOR校验XOR算法,最基本的bit运算法则为:
1⊕1 = 0, 0⊕0=0, 1⊕0=1;
因此,会衍生出如下的byte运算法则,对于byte数据M来说:
M⊕M=0, M⊕0=M;
从而如果P为数据块X,Y,Z计算的XOR 值,也就说P = X⊕Y⊕Z时;当X数据块不可用时,可以通过P,Y,Z来得到它,也就是
X = P⊕Y⊕Z = (X⊕Y⊕Z) ⊕Y⊕Z=X⊕(Y⊕Y) ⊕(Z⊕Z)
这就是基于XOR运算的RAID5能够允许一个存储设备故障的根本原因。
二、P+Q校验2.1 多个块同时写
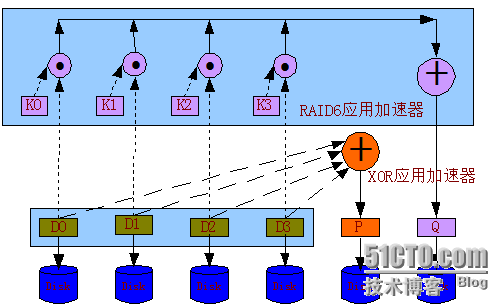
图-1 同时写多个块的P+Q校验
对于RAID6需要计算双重校验,第一重校验和RAID5一样,采用XOR校验,从上面的讲解可知,异或运算法则比较简单,所以可以设计专门的硬件来完成;在Intel的IOP33x处理器上就有专门的硬件模块,XOR应用加速器 (Application Accelerator with XOR),它专门处理异或运算,将CPU解放出来,从而提高整个系统的性能。如图-1,同时写多个数据块时,P = D0⊕D1⊕D2⊕D3,只需告诉XOR应用加速器D0, D1, D2, D3在内存的位置,它就可以自动的完成XOR计算得到P。
对于第二重校验,需要采用基于伽罗瓦域(Galois Field)计算操作的Reed- Solomon编码,也就是说在计算Q时,会引入一个系数Ki,如图-1所示:
Q = (K0⊙D0)⊕(K1⊙D1)⊕(K2⊙D2)⊕(K3⊙D3)
同样,由于RAID6采用了更为复杂的算法,因此可以设计专门的硬件来完成RAID6计算,Intel的IOP333上就有RAID6应用加速器 (Application Accelerator for RAID6);它和XOR应用加速器一样,只需要知道数据D0,D1,D2,D3在内存中的位置,它就可以自动完成RAID6的计算。
2.1 只写一个块
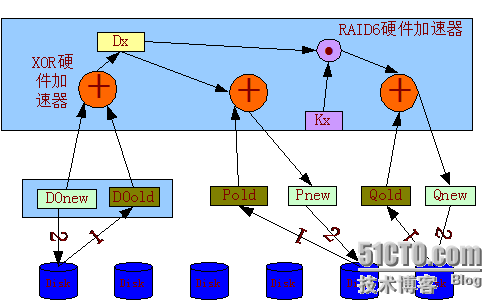
图-2 写一个块的P+Q校验
当系统只需要写一个数据块时,如果把所有的其他相关的数据块都读取出来计算校验,是比较耗费计算资源的。如图-2所示,此时先把需要写的块D0new对应的旧数据D0old读取,同时还有对应的Pold和Dold读取出来,从而可以得到如下公式:
Pnew = Pold ⊕ (D0new ⊕ D0old)
= (D0old⊕D1⊕D2⊕D3)⊕(D0new ⊕ D0old)
= D0new⊕D1⊕D2⊕D3
Qnew = Qold ⊕ Kx ⊙ (D0new⊕ D0old)
=(K0⊙D0)⊕(K1⊙D1)⊕(K2⊙D2)⊕(K3⊙D3)⊕Kx⊙(D0new⊕ D0old)
=(K0⊙D0)⊕(K1⊙D1)⊕(K2⊙D2)⊕(K3⊙D3)⊕K0⊙(D0new⊕ D0old)
=(K0⊙D0)⊕(K1⊙D1)⊕(K2⊙D2)⊕(K3⊙D3)
⊕(K0⊙D0new)⊕(K0⊙ D0old)
= (K1⊙D1)⊕(K2⊙D2)⊕(K3⊙D3)⊕(K0⊙D0new)
= (K0⊙D0new)⊕(K1⊙D1)⊕(K2⊙D2)⊕(K3⊙D3)
显然,通过上述只操作P和Q达到更新写一个块的数据,更为简洁高效。
三、里德--所罗门(Reed-Solomon)编码Reed-Solomon编码,是欧文.里德(Irving Reed)和格斯.所罗门(Gus Solomon)于1960年发布的一种纠错编码,它是最大距离可分码(MDS码,Maximum Distance Separable Code)的一种类型;表示为RS(n,k),其中n表示每个码字(codeword)符号的总数,k表示每个码字(codeword)中数据符号的总数
图-3 RS码字
其中2t = n – k,对于RAID6来说2t=2,所以它能修复两个磁盘损坏;如果符号(symbol)的长度为s,那么码字的长度n=2s – 1。Reed-Solomon编码将会用到伽罗瓦域(GF)运算法则,对于采用byte长度为Symbol,其最大码字长度为n = 28–1=255,所以它此时支持255个磁盘 ,其中253个为数据盘,剩下2个为校验盘,下面对该运算进行详细讲解。
四、伽罗瓦域(Galois Field)运算它包括+,-,×, ÷四种运算,其中+,-操作和XOR运算一样,表示为⊕;而×表示为乘以基数a,表示为⊙;同样,÷定义为,若A=C÷B,则C=A⊙B。
| 十进制整数 (常规数学运算) | 伽罗瓦域 (用XOR表示+) | ||
| 数 (十进制) | X=10 有效值={0…9} | 数 (二进制/十六进制) | X=a 有效值={0,1} |
| 256 | 2X2+5X1+6X0 | 1/0x1 | 1a0 |
| 15 | 1 X1+5 X0 | 101/0x5 | 1a2+0a1+1a0 |
| 求多项式的根 X2-3X1+2=0,X2=3X1+2 X={1,2} | 如果a为多项式 P(x)= X3+X1+1=0的根,那么由于+为XOR操作,所以a3=a1+1 | ||
| 推导公式: E0=1,En+1= En +1 | 推导公式: E0=a0,En+1= aEn |
表-1 十进制运算和伽罗瓦域运算对比
因此,可以得到GF(8)在产生多项式X8+ X4+ X3+ X2+1情况下的表:
| 多项式X8+ X4+ X3+ X2+1 | 求a8+ a4+ a3+ a2+1=0的根为 -> a8=a4+ a3+ a2+1 | HEX |
| 0 | 0 | 0h |
| a0 | 1 | 1h |
| a1 | a | 2h |
| a2 | a2 | 4h |
| a3 | a3 | 8h |
| a4 | a4 | 10h |
| a5 | a5 | 20h |
| a6 | a6 | 40h |
| a7 | a7 | 80h |
| a8 | a4+ a3+ a2+1 | 1dh |
| a9 | a(a4+ a3+ a2+1)= a5+ a4+ a3+a | 3ah |
| … | … | … |
表-2多项式X8+ X4+ X3+ X2+1的GF(8)表
从而得到该多项式GF(8)的运算表为:
| Gfilog(x)= ars | s | |||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | … | f | ||
| r | 0 | 1 | 2 | 4 | 8 | 10 | 20 | 40 | 80 | 1d | … | 26 |
| 1 | 4c | 98 | 2d | 5a | b4 | 75 | ea | c9 | 8f | … | c0 | |
| … |
表-3 GF(8)运算表
对应GF(8)的逆运算表GF-1(8)为
| Gflog(x)= ars | s | |||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | … | f | ||
| r | 0 | -- | 0 | 1 | 19 | 2 | 32 | 1a | c6 | 3 | … | 4b |
| 1 | 4 | 64 | e0 | e | 34 | 8d | ef | 81 | 1c | … | 71 | |
| … |
表-3 GF-1(8)运算表
从而,在GF运算将通过查表完成,如
2⊙8 = gfilog [gflog[2] + gflog[8] ] = gfilog[1+3]
= gfilog[4] = 0x10
五、RAID6的数据恢复5.1 P、Q故障
5.2 P与数据盘故障
5.3 Q与数据盘故障
5.4 两个数据盘故障
四、计算校验与性能关系内容
转载于:https://blog.51cto.com/luoqingchao/155088




 本文深入探讨了RAID6技术的原理,包括XOR校验、Reed-Solomon编码和伽罗瓦域运算等核心概念。介绍了在不同场景下如何进行数据块的写入与校验计算,并讨论了基于特定硬件加速器的应用。此外,还详细解释了Reed-Solomon编码及伽罗瓦域运算法则,以及这些技术如何帮助RAID6实现双磁盘冗余和数据恢复。
本文深入探讨了RAID6技术的原理,包括XOR校验、Reed-Solomon编码和伽罗瓦域运算等核心概念。介绍了在不同场景下如何进行数据块的写入与校验计算,并讨论了基于特定硬件加速器的应用。此外,还详细解释了Reed-Solomon编码及伽罗瓦域运算法则,以及这些技术如何帮助RAID6实现双磁盘冗余和数据恢复。
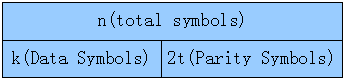
















 2953
2953

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








