浅谈基础算法之堆栈（五） - 川山甲 - 博客园

最新推荐文章于 2021-02-19 19:23:55 发布

weixin_33895016

最新推荐文章于 2021-02-19 19:23:55 发布

阅读量87

点赞数

浅谈基础算法之堆栈（五） - 川山甲 - 博客园

浅谈基础算法之堆栈（五）
目录

序

堆栈是什么？

实现方式

静态数组堆栈

动态数组堆栈

链式堆栈

总结

序

我一直在想一个问题，我怎么能把一件事情说的明白呢？尤其是程序方面的知识点。思路清楚是非常重要的（只有思路清楚，表达清楚了，才能一目了然），这个清楚的思路怎么表现出来？我努力去做这件事情。这篇主要围绕堆栈来展开话题。

堆栈是什么？
实现方式
静态数组堆栈

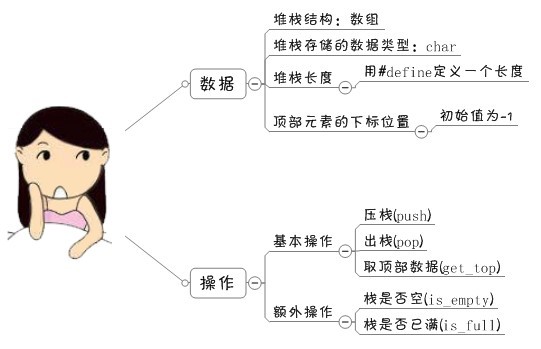1、先把你要做的事情准备好。
/* ===========数据 */
#define STACK_INIT_MAXSIZE 100
char stack[STACK_INIT_MAXSIZE];
int top = -1;


/* ===========操作  */
void push(){
}

void pop(){
}

char get_top(){
}

int is_empty(){
}

int is_full(){
}
这么一罗列，一下就明朗了！

2、开始逐步实现每一个函数。
/* 
 * 用一个静态数组实现堆栈
 *
 * (C) Copyright 2013 Chuan Shanjia
 */
#include <stdio.h>
#include <assert.h>


#define STACK_INIT_MAXSIZE 100
char stack[STACK_INIT_MAXSIZE];
int top = -1;


/* ===========基本操作  */
void push(char *value) {
    assert(!is_full());
    stack[++top] = *value;
}

void pop() {
    assert(!is_empty());
    top--;
}
char get_top() {
    assert(!is_empty());
    return stack[top];
}

/* ===========额外操作 */
int is_empty(){
    return top == -1;
}
int is_full(){
    return top == STACK_INIT_MAXSIZE - 1;
}
top存储堆栈顶部元素的下标值。开始由于没有顶部元素，所以初始值为-1，提示堆栈为空。

pop函数不需要从数组中删除元素，只减少顶部元素的下标值就足矣。

3、现在测试一下上面的堆栈的正确性（在上面的代码文件中，添加如下代码）。
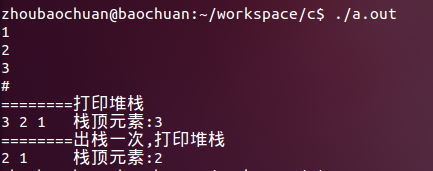
void print_stack(){
    int i = top;
    for(; i >= 0; i--){
        printf("%c ", stack[i]);
    }

    printf("\t");
    printf("栈顶元素:%c", get_top());
}

int main() {
    char c;
    scanf("%c", &c);
    while(c != '#'){
        if(c != '\n')
            push(&c);
        scanf("%c", &c);
    }

    printf("========打印堆栈\n");
    print_stack();
    printf("\n");

    printf("========出栈一次,打印堆栈\n");
    pop();
    print_stack();
    printf("\n");
    return 0;
}
打印结果如下：

动态数组堆栈

动态数组的特点：运行时才决定数组大小。——故需在原有的操作上，添加几个操作。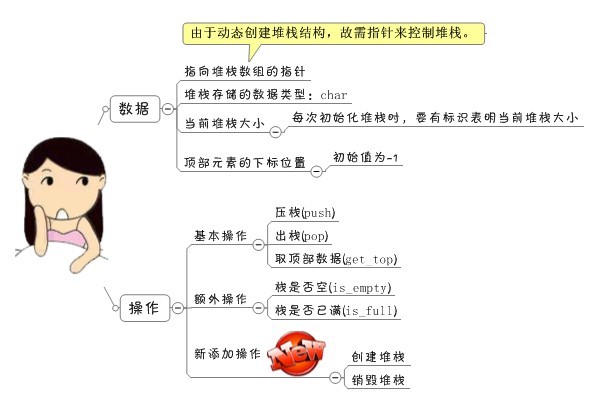

1、先把你要做的事情准备好。
/* ===========数据 */
char *stack;
int stack_size;
int top = -1;


/* ===========操作  */
void create_stack(){
}   

void destroy_stack(){
}   

void push(){
}

void pop(){
}

char get_top(){
}

int is_empty(){
}

int is_full(){
}
2、开始逐步实现每一个函数。
#include <stdio.h>
#include <assert.h>
#include <malloc.h>

/* ===========数据 */
char *stack;
int stack_size;
int top = -1;


/* ===========操作  */
void create_stack(int size){
    assert(size > 0); 
    stack_size = size;
    stack = (char *)malloc(stack_size * sizeof(char));
    assert(stack != NULL);
}

void destroy_stack(){
    assert(stack_size > 0); 
    free(stack);
    stack_size = 0;
    stack = NULL;
}

void push(char *value){
    assert(!is_full());
    stack[++top] = *value;
}

void pop(){
    assert(!is_empty());
    --top;
}

char get_top(){
    assert(!is_empty());
    return stack[top];
}

int is_empty(){
    assert(stack_size > 0);
    return top == -1;
}

int is_full(){
    assert(stack_size > 0);
    return top == stack_size - 1;
}
3、现在测试一下上面的堆栈的正确性（在上面的代码文件中，添加如下代码）。
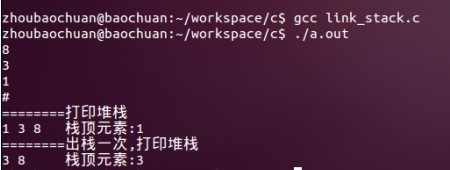
void print_stack(){
    int i = top;
    for(; i >= 0; i--){
        printf("%c ", stack[i]);
    }

    printf("\t");
    printf("栈顶元素:%c", get_top());
}

int main() {
    char c;
    create_stack(100);

    scanf("%c", &c);
    while(c != '#'){
        if(c != '\n')
            push(&c);
        scanf("%c", &c);
    }

    printf("========打印堆栈\n");
    print_stack();
    printf("\n");

    printf("========出栈一次,打印堆栈\n");
    pop();
    print_stack();
    printf("\n");

    destroy_stack();
    return 0;

}
打印结果如下：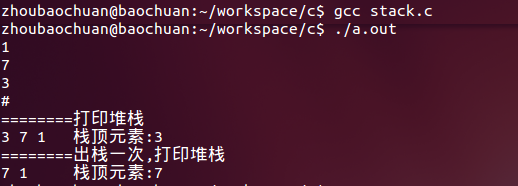
动态分配的链式结构堆栈（又名链式堆栈）

push和pop我们可以这样考虑，就是移动最后一个节点上的指针。push就把最后一个节点指针向后移动一位，pop就把指针向前移动一位。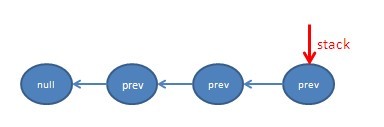

1、先把你要做的事情准备好。
struct stack_node{
    char data;
    struct stack_node *prev;
};

struct stack_node *current;

/* ===========基本操作  */
void push(){
}

void pop(){
}

char get_top(){
}

/* ===========额外操作 */
int is_empty(){
}
void destroy(){
}
2、开始逐步实现每一个函数。
#include <stdio.h>
#include <stdlib.h>
#include <assert.h>

struct stack_node{
    char data;
    struct stack_node *prev;
};

struct stack_node *current;

/* ===========基本操作  */
void push(char *value){
    struct stack_node *new = (struct stack_node *)malloc(sizeof(struct stack_node));
    assert(new != NULL);
    new->data = *value;
    new->prev = current;
    current = new;
}

void pop(){
    assert(!is_empty());
    struct stack_node *last_node = current;
    current = current->prev;
    free(last_node);
}   

char get_top(){
    assert(!is_empty());
    return current->data;
}

/* ===========额外操作 */
int is_empty(){
    return current == NULL;
}   

void destroy(){
    while(!is_empty()){
        pop();
    }
}
3、现在测试一下上面的堆栈的正确性（在上面的代码文件中，添加如下代码）。
void print_stack(){
    struct stack_node *print_node = current;
    while(print_node != NULL){
        printf("%c ", print_node->data);
        print_node = print_node->prev;
    }

    printf("\t");
    printf("栈顶元素:%c", get_top());
}
    
int main() {
    char c;
    
    scanf("%c", &c);
    while(c != '#'){
        if(c != '\n')
            push(&c);
        scanf("%c", &c);
    }
    
    printf("========打印堆栈\n");
    print_stack();
    printf("\n");

    printf("========出栈一次,打印堆栈\n");
    pop(); 
    print_stack();
    printf("\n");

    destroy_stack();
    return 0;

}
打印结果如下：
总结

以上三种方案我们要找到它们的特点：
静态数组堆栈要求结构的长度固定。而且这个要在编译时确定（我们用define定义）。——此方案最简单、最不容易出错。

动态数组堆栈我们可以在运行时才决定数组的长度。——在复杂性和平衡性之间做权衡。

链式结构堆栈每个元素在需要时才单独进行分配，这种方式对元素的数量几乎没有限制（排除考虑内存大小）。——最大程度的灵活性，需要消耗一定的内存，访问特定元素的效率不如数组。

最后，希望我的这篇博文对你有所帮助。

推荐
喜欢编程