【二项式定理】【推导】计蒜客17115 2017 ACM-ICPC 亚洲区（西安赛区）网络赛 B. Coin...

转载于 2017-09-16 19:02:00 发布 · 223 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/autsky-jadek/p/7532406.html

本文介绍了一个基于二项展开式计算投掷硬币出现偶数正面概率的问题，并提供了一段C++代码实现。通过使用快速幂运算，有效地解决了该概率计算问题。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题意：投一枚硬币向上的概率是q/p。问你投K枚硬币，向上的枚数为偶数枚的概率是？

要求的即为。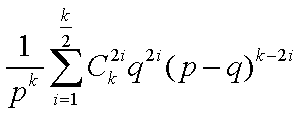

这个东西是个二项展开式的偶数项系数和，来，我们复习一下高中数学，设f(x)=(ax+b)^n，则其偶数项系数和为(f(1)+f(-1))/2。

#include<cstdio>
using namespace std;
typedef long long ll;
#define MOD 1000000007ll
int T;
ll p,q,K;
ll Quick_Pow(ll a,ll p,ll mod){
	if(!p){
		return 1ll;
	}
	ll res=Quick_Pow(a,p>>1,mod);
	res=res*res%mod;
	if((p&1ll)==1ll){
		res=(a%mod*res)%mod;
	}
	return res;
}
int main(){
	//freopen("b.in","r",stdin);
	scanf("%d",&T);
	for(;T;--T){
		scanf("%lld%lld%lld",&p,&q,&K);
		printf("%lld\n",(((Quick_Pow(p,K,MOD)+Quick_Pow(p-2ll*q,K,MOD))%MOD*Quick_Pow(2ll,MOD-2ll,MOD))%MOD
		*Quick_Pow(Quick_Pow(p,K,MOD),MOD-2ll,MOD))%MOD);
	}
	return 0;
}

转载于:https://www.cnblogs.com/autsky-jadek/p/7532406.html