[论文笔记] Fast Quality Driven Selection of Composite Web Services (ECOWS, 2006)

Time: 4.0 hours
Jae-Ho Jang, Dong-Hoon Shin, Kyong-Ho Lee, "Fast Quality Driven Selection of Composite Web Services," ecows, pp.87-98, Fourth IEEE European Conference on Web Services (ECOWS'06), 2006 (gs:1)

Google了一下作者Jae-Ho Jang, 发现返回的都是关于一个魔兽职业玩家的信息, 擅长使用精灵族. 应该不是同一个人. DBLP里作者只有这篇论文.
以下是论文笔记.

1. 这篇文章要解决的就是经典的QoS-aware service composition问题.
众所周知, 这个问题是NP难的, 随着成员服务和备选服务数量的增加, 求解花费的时间增长很快.
本文提出了一种将composite web service先分解(基于workflow partition strategy), 然后对每个partition进行服务选择的方法. 体现了朴素的divide and conquer思想.
针对的QoS包括: Latency, Cost, Reliability, Availability, Throughput, Capacity
针对的组合结构包括: Sequential, Parallel, Conditional, Loop

2. 本文的方法有以下几个关键点
(1) Partition abstract workflow into two sub-workflows
分解的好处就是能减少服务选择时间, 坏处就是不可避免地存在遗漏最优解的可能.
作者提出了"tightness of QoS requirement"的概念来控制这个坏处, 只有当一个workflow的tightnewss属性在规定门槛值之上时, 才进行划分.(详见第三点)

分解时, 首先要将workflow转化成Reduced Sequential Graph(RSG), 即只包含顺序结构. 做法很简单, 只是把分支结构视为一个节点而已. 例子如下图: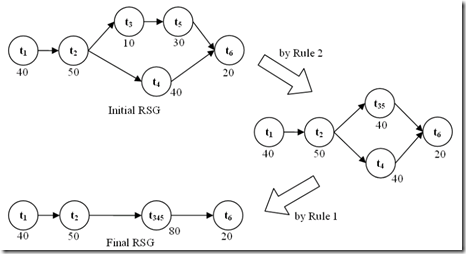

图中第一个图中t3和t5分别有10个和30个备选服务, 第二个图中t3和t5合并成t35, t35的标注的服务数量是40(是t3和t5备选服务简单相加), 显然, 这个40并不是备选服务的数量.
这种规约方法还有一个显而易见的缺点: 当非顺序结构占据了整个workflow的大部分时, 规约的意义就不大了.

规约之后, 由于只有顺序结构, 在划分时只需要考虑节点的数量, 不需要考虑结点之间的结构关系. 使用标准算法, 将这个节点集划分成最接近平分的两个子集(这种划分依据是否合理呢?)(如果两个子集包含的结点数目相差太大, 那么划分就是失败了).这两个子集就是sub-workflow.

(2) Decompose a QoS requirement for each sub-workflow
QoS分解公式如下, 具体推导过程见文中(S3.3)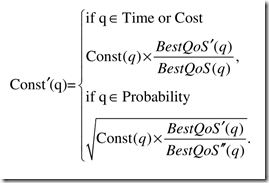
 
带'的是第一个workflow的属性, 带"的是第二个workflow的属性.

(3) Computing the tightness of a QoS requirement (S3.1)
定义: "the tightness represents the restrictiveness of the QoS requirement".
"Intuitively, as the requested level of QoS is increased, the number of composite Web services that meet the required QoS would decrease."
问题: "the number of composite Web services"怎么定义?

Tightness的计算方法如下:
首先, 每一个QoS的"tightness of constraint"都计算出来.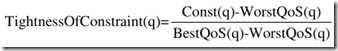
 
计算出来的所有QoS属性的TightnessOfConstraint值进行排序, 大的值排在前面(TightnessOfConstraint的值越大, 说明要求越高, 就越难满足).
排序后的结果放在Tightness数组里.

作者认为tightness of entire requirement主要是由最严格的QoS约束决定的, 因此使用了处理方法: "the tightness of a constraint is divided by the second power of its rank".
不知道这种处理方法是作者自己想出来的, 还是说本来就有的? 有什么特性?
如果将TightnessOfRequirement直接定义为Tightness之和, 本身也能体现出最严格的QoS约束值越大的特点, 有什么不好?

3. (S3.4)是用MILP方法来解决QoS aware service composition问题的套路
objective用的是Zeng04的那一套. 细节方面与Zeng04有所不同, 有必要可以再细看.

4. 勘误
公式3中, Probability那一行, "QoS'(q) + QoS"(q)"应该是"QoS'(q) * QoS"(q)"

转载于:https://www.cnblogs.com/yuquanlaobo/archive/2009/08/25/1552361.html