5.1 一些简单的标记
marker description
”.” point
”,” pixel
“o” circle
“v” triangle_down
“^” triangle_up
“<” triangle_left
“>” triangle_right
“1” tri_down
“2” tri_up
“3” tri_left
“4” tri_right
“8” octagon
“s” square
“p” pentagon
“*” star
“h” hexagon1
“H” hexagon2
“+” plus
“x” x
“D” diamond
“d” thin_diamond
“|” vline
“_” hline
5.2 生成简单的二维矩阵
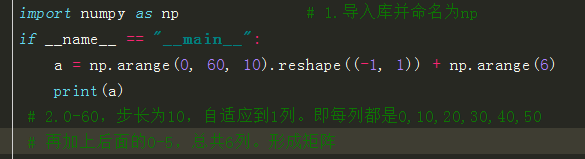
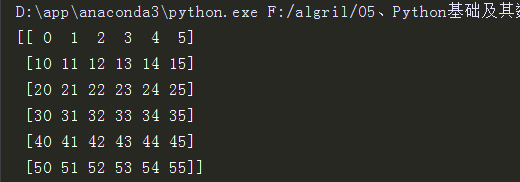
# 正式开始 -:)
# 标准Python的列表(list)中,元素本质是对象。
# 如:L = [1, 2, 3],需要3个指针和三个整数对象,对于数值运算比较浪费内存和CPU。
# 因此,Numpy提供了ndarray(N-dimensional array object)对象:存储单一数据类型的多维数组。
2. 多维数组


import numpy as np # 1.导入库并命名为np if __name__ == "__main__": # # 1.使用array创建 # 通过array函数传递list对象 L = [1, 2, 3, 4, 5, 6] print("L = ", L) a = np.array(L) print("a = ", a) print(type(a)) # 若传递的是多层嵌套的list,将创建多维数组 b = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]]) print(b)

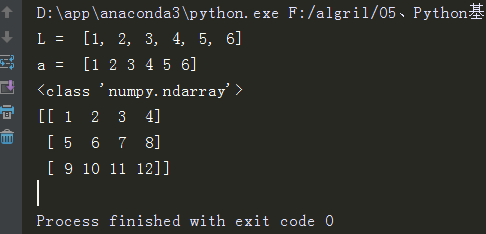
3.
# 1.使用array创建,通过array函数传递list对象
# 2.若传递的是多层嵌套的list,将创建多维数组
# 3.数组大小可以通过其shape属性获得
# 4.也可以强制修改shape
# 5.当某个轴为-1时,将根据数组元素的个数自动计算此轴的长度
# 6.使用reshape方法,可以创建改变了尺寸的新数组,原数组的shape保持不变
# 7.数组b和c共享内存,修改任意一个将影响另外一个
# 8.数组的元素类型可以通过dtype属性获得
# 9.可以通过dtype参数在创建时指定元素类型
# 10.如果更改元素类型,可以使用astype安全的转换

import numpy as np # 1.导入库并命名为np if __name__ == "__main__": # 1.使用array创建,通过array函数传递list对象 L = [1, 2, 3, 4, 5, 6] a = np.array(L) print("a = ", a, 'a的类型:',type(a)) # 2.若传递的是多层嵌套的list,将创建多维数组 b = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]]) print(b) # 3.数组大小可以通过其shape属性获得 print('a的大小=',a.shape,'b的大小=',b.shape) # 4.也可以强制修改shape b.shape = 4, 3 print(b) #注:从(3,4)改为(4,3)并不是对数组进行转置,而只是改变每个轴的大小,数组元素在内存中的位置并没有改变 # 5.当某个轴为-1时,将根据数组元素的个数自动计算此轴的长度 b.shape = 2, -1 print(b) print(b.shape) # # b.shape = 3, 4 # 6.使用reshape方法,可以创建改变了尺寸的新数组,原数组的shape保持不变 c = b.reshape((4, -1)) print("b = \n", b) print('c = \n', c) # 7.数组b和c共享内存,修改任意一个将影响另外一个 b[0][1] = 20 print("b = \n", b) print("c = \n", c) # # # 8.数组的元素类型可以通过dtype属性获得 print(a.dtype) print(b.dtype) # 9.可以通过dtype参数在创建时指定元素类型 d = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]], dtype=np.float) f = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]], dtype=np.complex) print(d,'\n',f) # 10.如果更改元素类型,可以使用astype安全的转换 f = d.astype(np.int) print(f) # 但不要强制仅修改元素类型,如下面这句,将会以int来解释单精度float类型 d.dtype = np.int print(d)
4. 使用函数创建
# 2.2arange函数类似于python的range函数:指定起始值、终止值和步长来创建数组,arange同样不包括终值;但arange可以生成浮点类型,而range只能是整数类型
# 2.3linspace函数通过指定起始值、终止值和元素个数来创建数组,缺省包括终止值
# 2.4可以通过endpoint关键字指定是否包括终值
# 2.5和linspace类似,logspace可以创建等比数列,下面函数创建起始值为10^1,终止值为10^2,有20个数的等比数列
# 2.6下面创建起始值为2^0,终止值为2^10(包括),有10个数的等比数列
# 2.7使用frombuffer, fromstring, fromfile等函数可以从字节序列创建数组


import numpy as np # 1.导入库并命名为np if __name__ == "__main__": # 2.使用函数创建 # 2.1如果生成一定规则的数据,可以使用NumPy提供的专门函数 # 2.2arange函数类似于python的range函数:指定起始值、终止值和步长来创建数组,arange同样不包括终值;但arange可以生成浮点类型,而range只能是整数类型 a = np.arange(1, 10, 0.5) print(a) # 2.3linspace函数通过指定起始值、终止值和元素个数来创建数组,缺省包括终止值 b = np.linspace(1, 10, 10) print('b = ', b) # 2.4可以通过endpoint关键字指定是否包括终值 c = np.linspace(1, 10, 10, endpoint=False) print('c = ', c) # 2.5和linspace类似,logspace可以创建等比数列,下面函数创建起始值为10^1,终止值为10^2,有20个数的等比数列 d = np.logspace(1, 2, 10, endpoint=True) print(d) # 2.6下面创建起始值为2^0,终止值为2^10(包括),有10个数的等比数列 f = np.logspace(0, 10, 10, endpoint=True, base=2) print(f) # 2.7使用frombuffer, fromstring, fromfile等函数可以从字节序列创建数组 s = 'abcd' g = np.fromstring(s, dtype=np.int8) print(g)
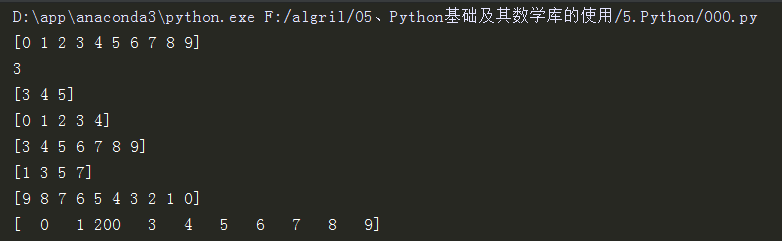
5.存取。 数组元素的存取方法和Python的标准方法相同


import numpy as np # 1.导入库并命名为np if __name__ == "__main__": # 3.存取。 数组元素的存取方法和Python的标准方法相同 a = np.arange(10) #注意是从0到9 print(a) print(a[3]) # 获取某个元素,下标从0开始 print(a[3:6]) # 切片[3,6),左闭右开 print(a[:5]) print(a[3:]) # 下标为负表示从后向前数 print(a[1:9:2]) # 步长为2 print(a[::-1]) # 步长为-1,即翻转 #原始数据是否被破坏,如: b = a[2:5] b[0] = 200 print(a)
6.

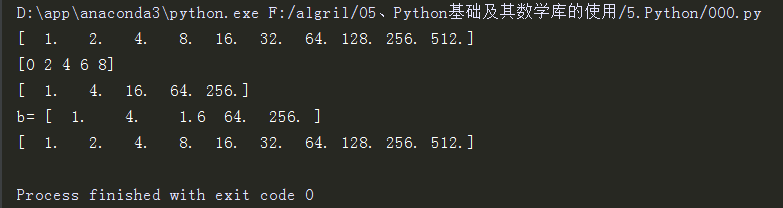


import numpy as np # 1.导入库并命名为np if __name__ == "__main__": # # 3.2 整数/布尔数组存取 # 根据整数数组存取:当使用整数序列对数组元素进行存取时, # 将使用整数序列中的每个元素作为下标,整数序列可以是列表(list)或者数组(ndarray)。 # 使用整数序列作为下标获得的数组不和原始数组共享数据空间。 a = np.logspace(0, 9, 10, base=2) print(a) i = np.arange(0, 10, 2) print(i) # 利用i取a中的元素 b = a[i] print(b) # b的元素更改,a中元素不受影响 b[2] = 1.6 print('b=',b) print(a)
7.
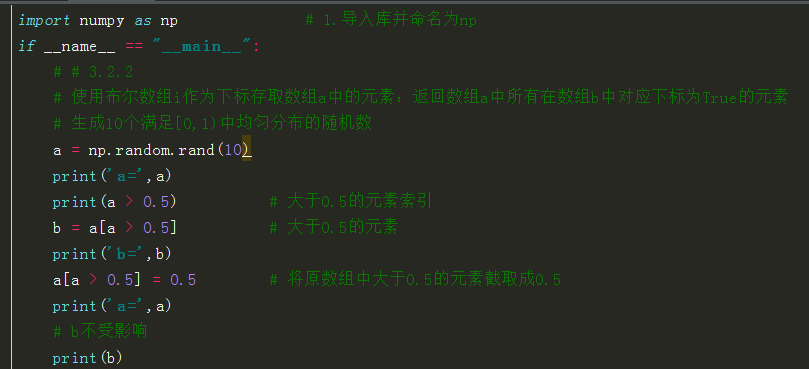
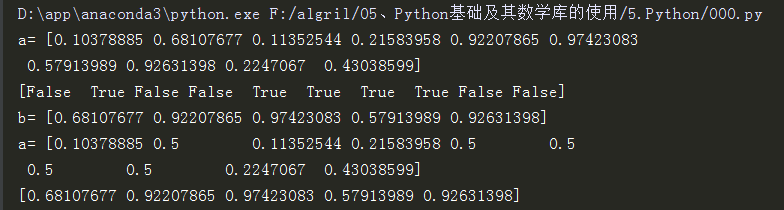


import numpy as np # 1.导入库并命名为np if __name__ == "__main__": # # 3.2.2 # 使用布尔数组i作为下标存取数组a中的元素:返回数组a中所有在数组b中对应下标为True的元素 # 生成10个满足[0,1)中均匀分布的随机数 a = np.random.rand(10) print('a=',a) print(a > 0.5) # 大于0.5的元素索引 b = a[a > 0.5] # 大于0.5的元素 print('b=',b) a[a > 0.5] = 0.5 # 将原数组中大于0.5的元素截取成0.5 print('a=',a) # b不受影响 print(b)
8.
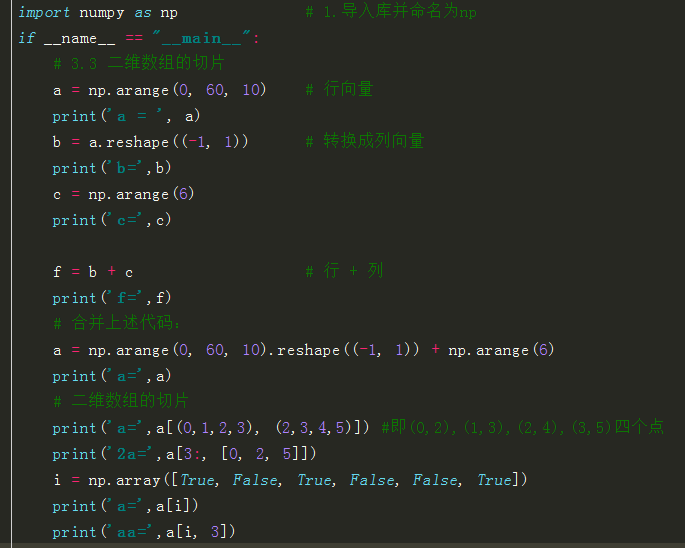


import numpy as np # 1.导入库并命名为np if __name__ == "__main__": # 3.3 二维数组的切片 a = np.arange(0, 60, 10) # 行向量 print('a = ', a) b = a.reshape((-1, 1)) # 转换成列向量 print('b=',b) c = np.arange(6) print('c=',c) f = b + c # 行 + 列 print('f=',f) # 合并上述代码: a = np.arange(0, 60, 10).reshape((-1, 1)) + np.arange(6) print('a=',a) # 二维数组的切片 print('a=',a[(0,1,2,3), (2,3,4,5)]) #即(0,2),(1,3),(2,4),(3,5)四个点 print('2a=',a[3:, [0, 2, 5]]) i = np.array([True, False, True, False, False, True]) print('a=',a[i]) print('aa=',a[i, 3])
10. 绘图
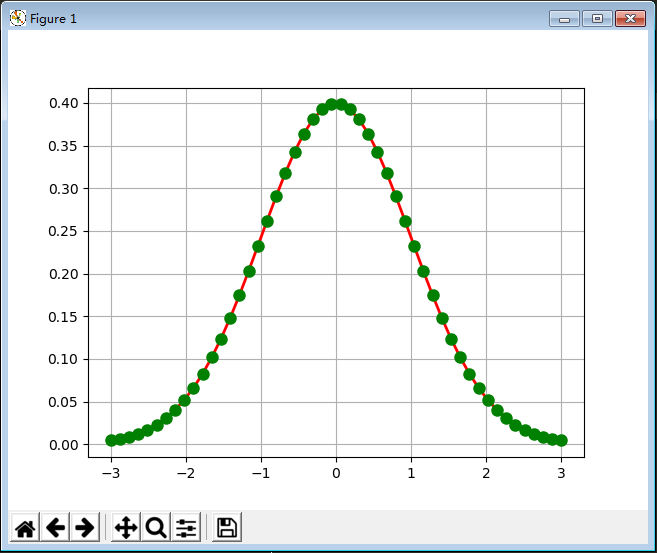


import numpy as np # 1.导入库并命名为np import matplotlib import matplotlib.pyplot as plt import math if __name__ == "__main__": # 5.绘图 # 5.1 绘制正态分布概率密度函数 mu = 0 sigma = 1 x = np.linspace(mu - 3 * sigma, mu + 3 * sigma, 50) y = np.exp(-(x - mu) ** 2 / (2 * sigma ** 2)) / (math.sqrt(2 * math.pi) * sigma) # 正态分布 print(x.shape) # x 的大小 print('x = \n', x) print(y.shape) # y 的大小 print('y = \n', y) # plt.plot(x, y, 'ro-', linewidth=2) plt.plot(x, y, 'r-', x, y, 'go', linewidth=2, markersize=8) plt.grid(True) # 画网格 plt.show() matplotlib.rcParams['font.sans-serif'] = [u'SimHei'] # FangSong/黑体 FangSong/KaiTi matplotlib.rcParams['axes.unicode_minus'] = False
11. 损失函数
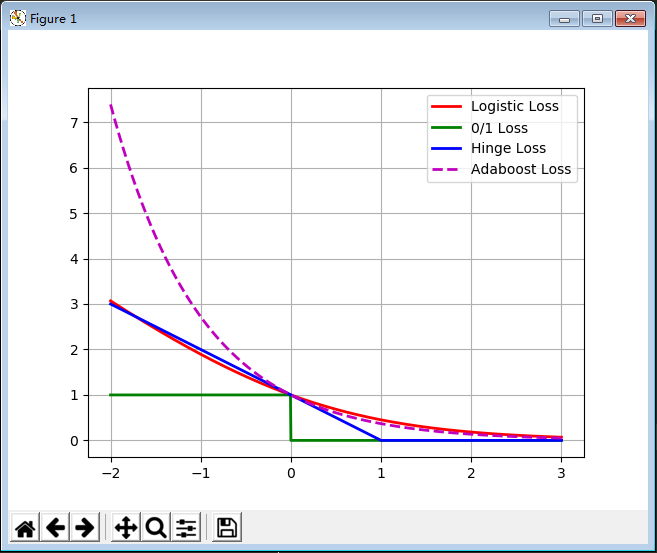


import numpy as np # 1.导入库并命名为np import matplotlib import matplotlib.pyplot as plt import math if __name__ == "__main__": # 5.2 损失函数:Logistic损失(-1,1)/SVM Hinge损失/ 0/1损失 x = np.array(np.linspace(start=-2, stop=3, num=1001, dtype=np.float)) y_logit = np.log(1 + np.exp(-x)) / math.log(2) y_boost = np.exp(-x) y_01 = x < 0 y_hinge = 1.0 - x # y = -x +1 的直线 y_hinge[y_hinge < 0] = 0 # 直线y = -x +1小于0,则x > 1,令y_hinge[x > 1] = 0 plt.plot(x, y_logit, 'r-', label='Logistic Loss', linewidth=2) plt.plot(x, y_01, 'g-', label='0/1 Loss', linewidth=2) # label标签,在图片右上角打印标签 plt.plot(x, y_hinge, 'b-', label='Hinge Loss', linewidth=2) plt.plot(x, y_boost, 'm--', label='Adaboost Loss', linewidth=2) plt.grid() plt.legend(loc='upper right') # plt.savefig('1.png') # 保存为照片 plt.show()
12. 画出x^x的曲线。 (1.导包numpy,matplotlib ;2.定义f(x) ; 3.画图)
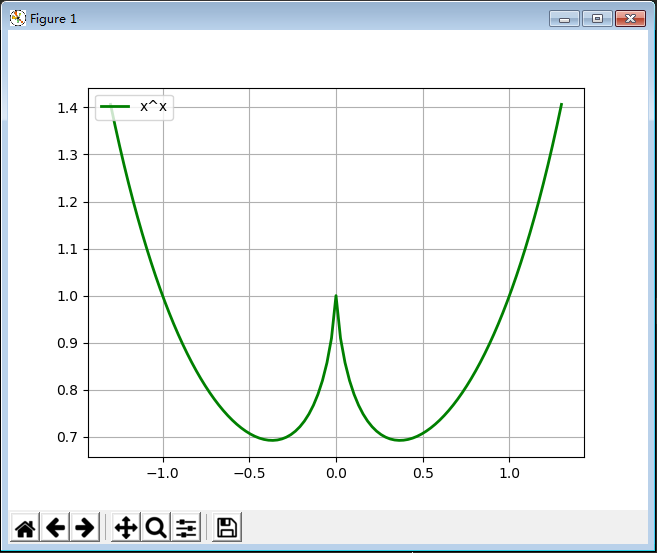


import numpy as np # 1.导入库并命名为np import matplotlib import matplotlib.pyplot as plt import math def f(x): y = np.ones_like(x) # 返回一个用1填充的跟输入形状和类型 一致的数组。 i = x > 0 # 同理,zeros_like返回一个用0填充的跟输入数组 形状和类型一样的数组。 y[i] = np.power(x[i], x[i]) i = x < 0 y[i] = np.power(-x[i], -x[i]) return y if __name__ == "__main__": # # # 5.3 x^x x = np.linspace(-1.3, 1.3, 101) y = f(x) plt.plot(x, y, 'g-', label='x^x', linewidth=2) plt.grid() # 网格 plt.legend(loc='upper left') # label='x^x'的标签放在左上角 plt.show()
13 胸型线
figure的基本语法:详见: https://blog.youkuaiyun.com/m0_37362454/article/details/81511427



import numpy as np import matplotlib from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm import time from scipy.optimize import leastsq import scipy.optimize as opt import scipy import matplotlib.pyplot as plt from scipy.stats import norm, poisson from scipy.interpolate import BarycentricInterpolator from scipy.interpolate import CubicSpline import math if __name__ == "__main__": # 5.4 胸型线 x = np.arange(1,0,-0.001) # 从1到0,步长为 倒着的0.001 y = (-3 * x * np.log(x) + np.exp(-(40 * (x - 1 / np.e)) ** 4) / 25) / 2 plt.figure(figsize=(5,7)) # 指定figure的宽和高 plt.plot(y, x, 'r-', linewidth=2) plt.grid(True) plt.show()
13 心形线
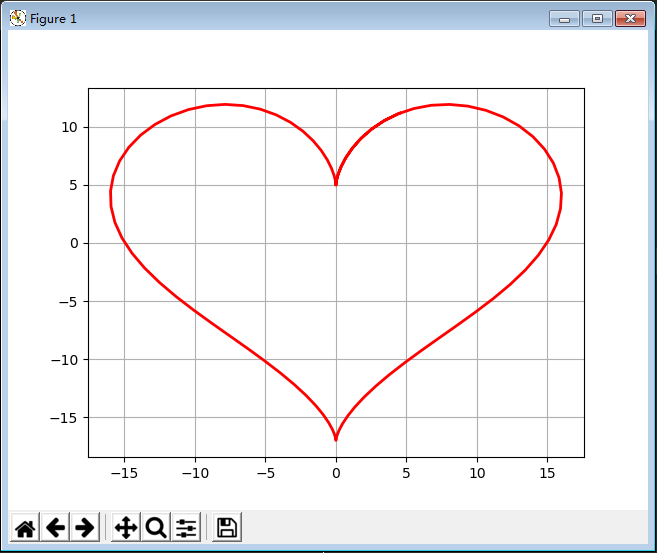


import numpy as np import matplotlib from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm import time from scipy.optimize import leastsq import scipy.optimize as opt import scipy import matplotlib.pyplot as plt from scipy.stats import norm, poisson from scipy.interpolate import BarycentricInterpolator from scipy.interpolate import CubicSpline import math if __name__ == "__main__": # 5.5 心形线 t = np.linspace(0, 7, 100) x = 16 * np.sin(t) ** 3 y = 13 * np.cos(t) - 5 * np.cos(2*t) - 2 * np.cos(3*t) - np.cos(4*t) plt.plot(x, y, 'r-', linewidth=2) plt.grid(True) plt.show()
14 渐开线
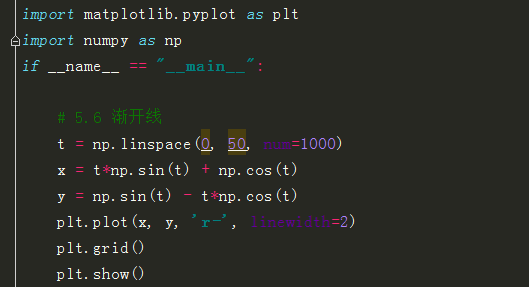
15 Bar
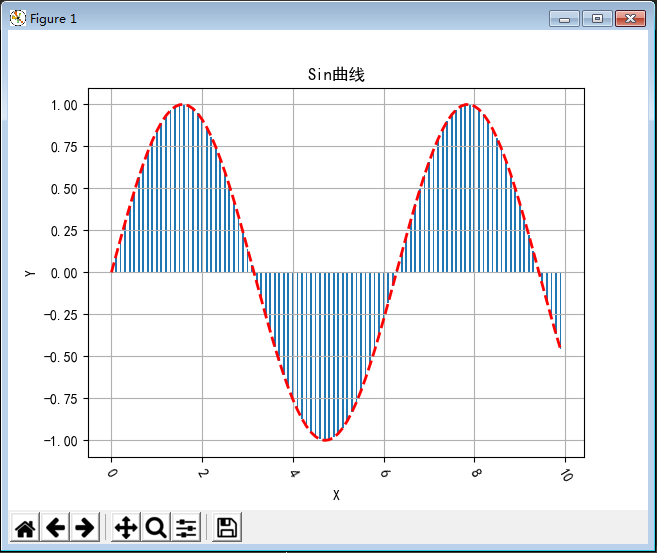


import matplotlib import matplotlib.pyplot as plt import numpy as np if __name__ == "__main__": # # Bar matplotlib.rcParams['font.sans-serif'] = [u'SimHei'] #黑体 FangSong/KaiTi matplotlib.rcParams['axes.unicode_minus'] = False x = np.arange(0, 10, 0.1) y = np.sin(x) plt.bar(x, y, width=0.04, linewidth=0.2) plt.plot(x, y, 'r--', linewidth=2) plt.title(u'Sin曲线') plt.xticks(rotation=-60) plt.xlabel('X') plt.ylabel('Y') plt.grid() plt.show()
16 概率分布
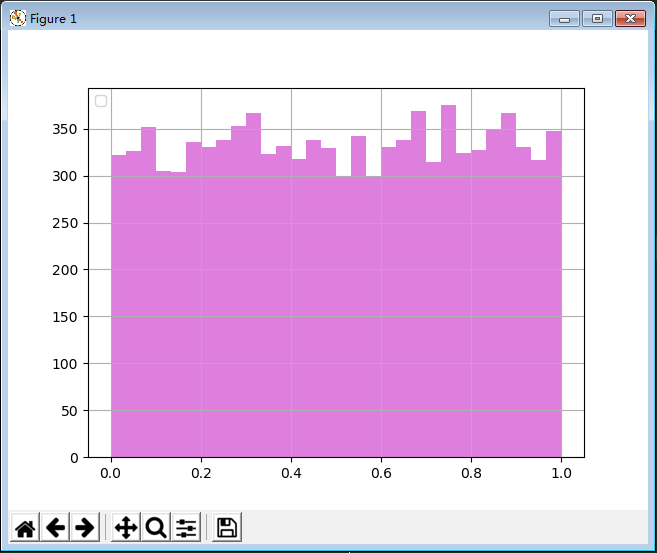


import matplotlib.pyplot as plt import numpy as np if __name__ == "__main__": # 6. 概率分布 # 6.1 均匀分布 x = np.random.rand(10000) t = np.arange(len(x)) plt.hist(x, 30, color='m', alpha=0.5) # plt.plot(t, x, 'r-', label=u'均匀分布') plt.legend(loc='upper left') plt.grid() plt.show()
17. 中心极限定理
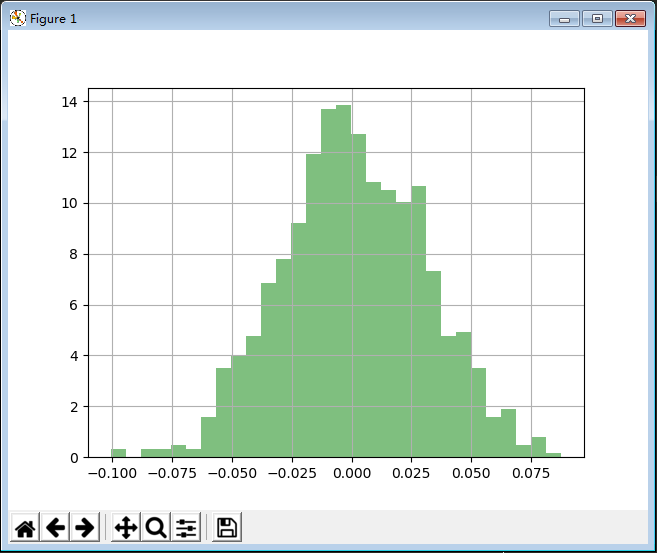


import matplotlib.pyplot as plt import numpy as np if __name__ == "__main__": # # 6.2 验证中心极限定理 t = 10000 a = np.zeros(1000) for i in range(t): a += np.random.uniform(-5, 5, 1000) a /= t plt.hist(a, bins=30, color='g', alpha=0.5, normed=True) plt.grid() plt.show()
18 Poisson分布 直方图


from scipy.stats import norm, poisson import matplotlib.pyplot as plt import numpy as np if __name__ == "__main__": # 6.3 Poisson分布 x = np.random.poisson(lam=5, size=10000) print(x) pillar = 15 a = plt.hist(x, bins=pillar, normed=True, range=[0, pillar], color='g', alpha=0.5) plt.grid() # plt.show() print(a) print(a[0].sum()) # 6.4 直方图的使用 mu = 2 sigma = 3 data = mu + sigma * np.random.randn(1000) h = plt.hist(data, 30, normed=1, color='#a0a0ff') x = h[1] y = norm.pdf(x, loc=mu, scale=sigma) plt.plot(x, y, 'r--', x, y, 'ro', linewidth=2, markersize=4) plt.grid() plt.show()
19 插值
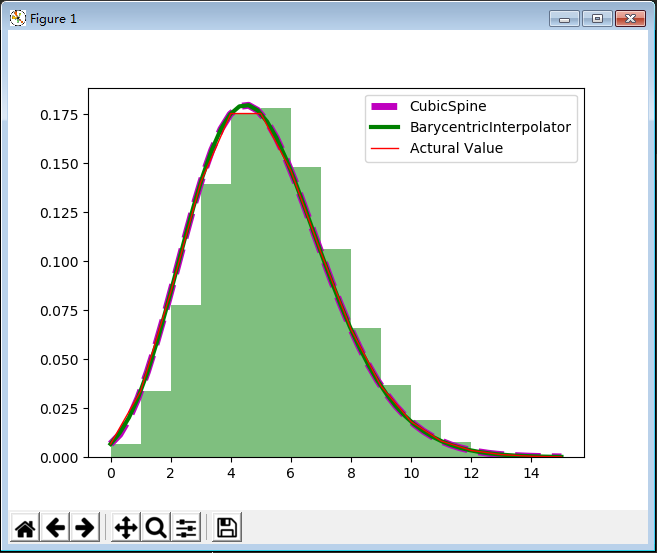


import scipy from scipy.interpolate import BarycentricInterpolator from scipy.interpolate import CubicSpline import math from scipy.stats import norm, poisson import matplotlib.pyplot as plt import numpy as np if __name__ == "__main__": # 6.3 Poisson分布 x = np.random.poisson(lam=5, size=10000) pillar = 15 a = plt.hist(x, bins=pillar, density=True, range=[0, pillar], color='g', alpha=0.5) plt.grid() # plt.show() print(a[0].sum()) # 6.5 插值 rv = poisson(5) x1 = a[1] y1 = rv.pmf(x1) itp = BarycentricInterpolator(x1, y1) # 重心插值 x2 = np.linspace(x.min(), x.max(), 50) y2 = itp(x2) cs = scipy.interpolate.CubicSpline(x1, y1) # 三次样条插值 plt.plot(x2, cs(x2), 'm--', linewidth=5, label='CubicSpine') # 三次样条插值 plt.plot(x2, y2, 'g-', linewidth=3, label='BarycentricInterpolator') # 重心插值 plt.plot(x1, y1, 'r-', linewidth=1, label='Actural Value') # 原始值 plt.legend(loc='upper right') plt.grid() plt.show()
19 三维图形
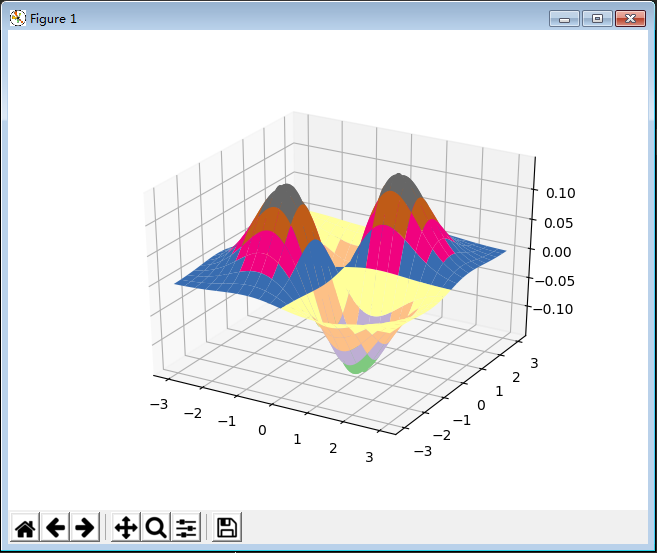


import math from scipy.stats import norm, poisson import matplotlib.pyplot as plt from matplotlib import cm import numpy as np if __name__ == "__main__": # 7. 绘制三维图像 x, y = np.ogrid[-3:3:100j, -3:3:100j] z = x*y*np.exp(-(x**2 + y**2)/2) / math.sqrt(2*math.pi) # z = x*y*np.exp(-(x**2 + y**2)/2) / math.sqrt(2*math.pi) fig = plt.figure() ax = fig.add_subplot(111, projection='3d') # ax.plot_surface(x, y, z, rstride=5, cstride=5, cmap=cm.coolwarm, linewidth=0.1) # ax.plot_surface(x, y, z, rstride=5, cstride=5, cmap=cm.Accent, linewidth=0.5) plt.show()
20.线性回归 首先定义residual方法。
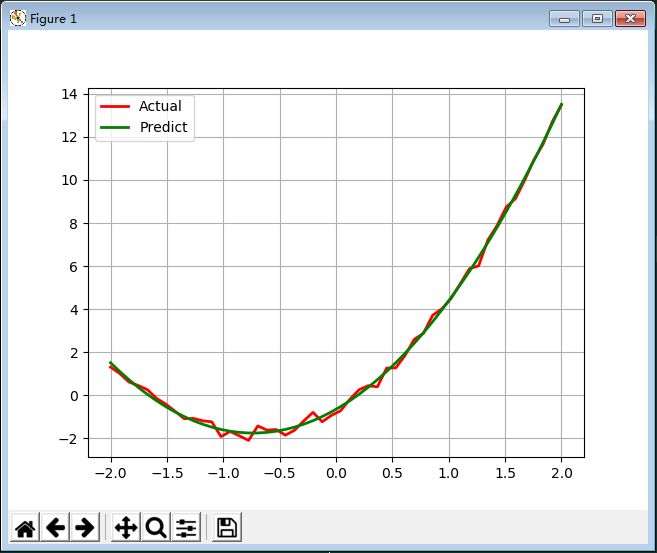


import matplotlib.pyplot as plt from scipy.optimize import leastsq import numpy as np def residual(t, x, y): return y - (t[0] * x ** 2 + t[1] * x + t[2]) if __name__ == "__main__": # 8.1 scipy 线性回归例1 x = np.linspace(-2, 2, 50) A, B, C = 2, 3, -1 y = (A * x ** 2 + B * x + C) + np.random.rand(len(x))*0.75 t = leastsq(residual, [0, 0, 0], args=(x, y)) theta = t[0] print('真实值:', A, B, C) print('预测值:', theta) y_hat = theta[0] * x ** 2 + theta[1] * x + theta[2] plt.plot(x, y, 'r-', linewidth=2, label=u'Actual') plt.plot(x, y_hat, 'g-', linewidth=2, label=u'Predict') plt.legend(loc='upper left') plt.grid() plt.show() import matplotlib.pyplot as plt from scipy.optimize import leastsq import numpy as np def residual(t, x, y): return y - (t[0] * x ** 2 + t[1] * x + t[2]) if __name__ == "__main__": # 8.1 scipy 线性回归例1 x = np.linspace(-2, 2, 50) A, B, C = 2, 3, -1 y = (A * x ** 2 + B * x + C) + np.random.rand(len(x))*0.75 t = leastsq(residual, [0, 0, 0], args=(x, y)) theta = t[0] print('真实值:', A, B, C) print('预测值:', theta) y_hat = theta[0] * x ** 2 + theta[1] * x + theta[2] plt.plot(x, y, 'r-', linewidth=2, label=u'Actual') plt.plot(x, y_hat, 'g-', linewidth=2, label=u'Predict') plt.legend(loc='upper left') plt.grid() plt.show()
21
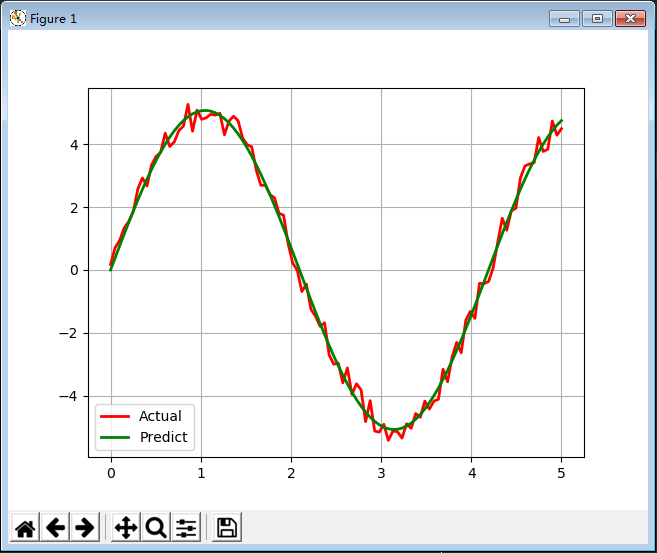


def residual2(t, x, y): print(t[0], t[1]) return y - t[0]*np.sin(t[1]*x) import matplotlib.pyplot as plt from scipy.optimize import leastsq import numpy as np if __name__ == "__main__": # 线性回归例2 x = np.linspace(0, 5, 100) A = 5 w = 1.5 y = A * np.sin(w*x) + np.random.rand(len(x)) - 0.5 t = leastsq(residual2, [3, 1], args=(x, y)) theta = t[0] print('真实值:', A, w) print('预测值:', theta) y_hat = theta[0] * np.sin(theta[1] * x) plt.plot(x, y, 'r-', linewidth=2, label='Actual') plt.plot(x, y_hat, 'g-', linewidth=2, label='Predict') plt.legend(loc='lower left') plt.grid() plt.show()
==============5.2====================
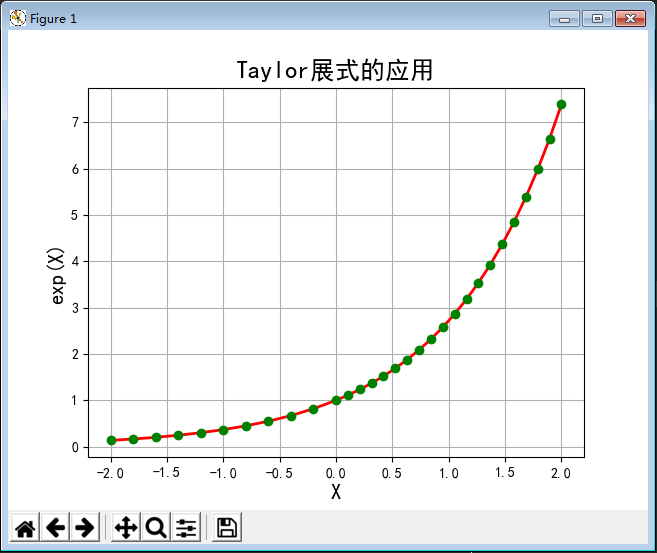


#!/usr/bin/python # -*- coding:utf-8 -*- import numpy as np import math import matplotlib as mpl import matplotlib.pyplot as plt def calc_e_small(x): n = 10 f = np.arange(1, n+1).cumprod() b = np.array([x]*n).cumprod() return np.sum(b / f) + 1 def calc_e(x): reverse = False if x < 0: # 处理负数 x = -x reverse = True ln2 = 0.69314718055994530941723212145818 c = x / ln2 a = int(c+0.5) b = x - a*ln2 y = (2 ** a) * calc_e_small(b) if reverse: return 1/y return y if __name__ == "__main__": t1 = np.linspace(-2, 0, 10, endpoint=False) t2 = np.linspace(0, 2, 20) t = np.concatenate((t1, t2)) print(t ) # 横轴数据 y = np.empty_like(t) for i, x in enumerate(t): y[i] = calc_e(x) print('e^', x, ' = ', y[i], '(近似值)\t', math.exp(x), '(真实值)') # print '误差:', y[i] - math.exp(x) mpl.rcParams['font.sans-serif'] = [u'SimHei'] mpl.rcParams['axes.unicode_minus'] = False plt.plot(t, y, 'r-', t, y, 'go', linewidth=2) plt.title(u'Taylor展式的应用', fontsize=18) plt.xlabel('X', fontsize=15) plt.ylabel('exp(X)', fontsize=15) plt.grid(True) plt.show()
======================


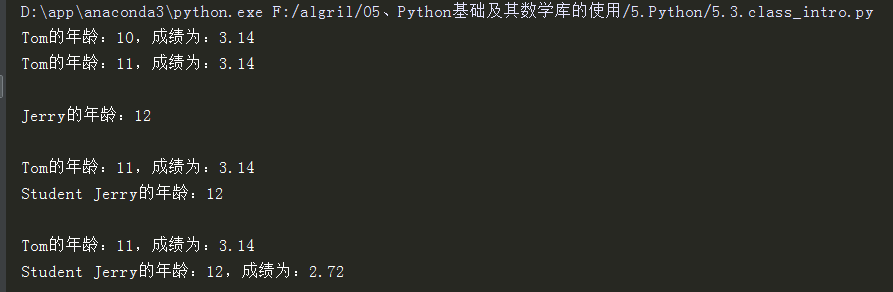
#!/usr/bin/python # -*- coding:utf-8 -*- class People: def __init__(self, n, a, s): self.name = n self.age = a self.__score = s self.print_people() # self.__print_people() # 私有函数的作用 def print_people(self): str = u'%s的年龄:%d,成绩为:%.2f' % (self.name, self.age, self.__score) print(str) __print_people = print_people class Student(People): def __init__(self, n, a, w): People.__init__(self, n, a, w) self.name = 'Student ' + self.name def print_people(self): str = u'%s的年龄:%d' % (self.name, self.age) print(str) def func(p): p.age = 11 if __name__ == '__main__': p = People('Tom', 10, 3.14159) func(p) # p传入的是引用类型 p.print_people() print() # 注意分析下面语句的打印结果,是否觉得有些“怪异”? j = Student('Jerry', 12, 2.71828) print() # 成员函数 p.print_people() j.print_people() print() People.print_people(p) People.print_people(j)
=======================


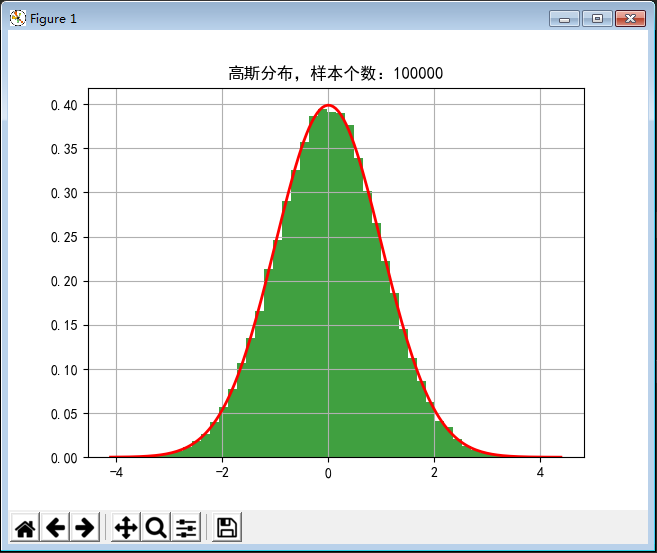
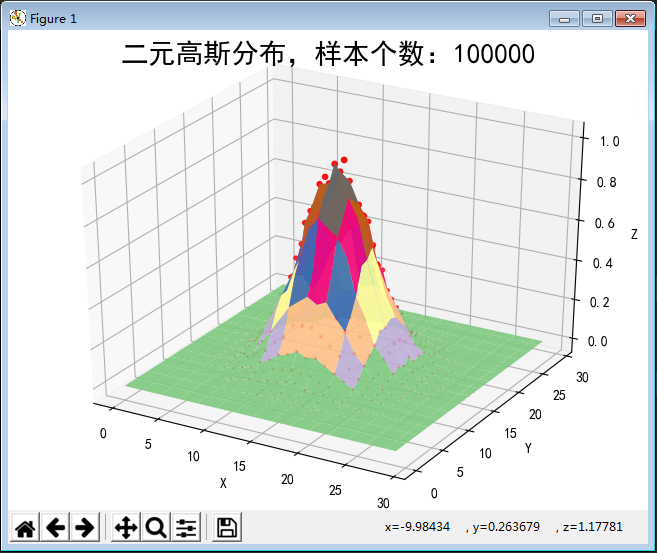
#!/usr/bin/python # -*- coding:utf-8 -*- import numpy as np from scipy import stats import math import matplotlib as mpl import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm def calc_statistics(x): n = x.shape[0] # 样本个数 # 手动计算 m = 0 m2 = 0 m3 = 0 m4 = 0 for t in x: m += t m2 += t*t m3 += t**3 m4 += t**4 m /= n m2 /= n m3 /= n m4 /= n mu = m sigma = np.sqrt(m2 - mu*mu) skew = (m3 - 3*mu*m2 + 2*mu**3) / sigma**3 kurtosis = (m4 - 4*mu*m3 + 6*mu*mu*m2 - 4*mu**3*mu + mu**4) / sigma**4 - 3 print('手动计算均值、标准差、偏度、峰度:', mu, sigma, skew, kurtosis) # 使用系统函数验证 mu = np.mean(x, axis=0) sigma = np.std(x, axis=0) skew = stats.skew(x) kurtosis = stats.kurtosis(x) return mu, sigma, skew, kurtosis if __name__ == '__main__': d = np.random.randn(100000) print(d) mu, sigma, skew, kurtosis = calc_statistics(d) print('函数库计算均值、标准差、偏度、峰度:', mu, sigma, skew, kurtosis) # 一维直方图 mpl.rcParams[u'font.sans-serif'] = 'SimHei' mpl.rcParams[u'axes.unicode_minus'] = False y1, x1, dummy = plt.hist(d, bins=50, normed=True, color='g', alpha=0.75) t = np.arange(x1.min(), x1.max(), 0.05) y = np.exp(-t**2 / 2) / math.sqrt(2*math.pi) plt.plot(t, y, 'r-', lw=2) plt.title(u'高斯分布,样本个数:%d' % d.shape[0]) plt.grid(True) plt.show() d = np.random.randn(100000, 2) mu, sigma, skew, kurtosis = calc_statistics(d) print('函数库计算均值、标准差、偏度、峰度:', mu, sigma, skew, kurtosis) # 二维图像 N = 30 density, edges = np.histogramdd(d, bins=[N, N]) print('样本总数:', np.sum(density)) density /= density.max() x = y = np.arange(N) t = np.meshgrid(x, y) fig = plt.figure(facecolor='w') ax = fig.add_subplot(111, projection='3d') ax.scatter(t[0], t[1], density, c='r', s=15*density, marker='o', depthshade=True) ax.plot_surface(t[0], t[1], density, cmap=cm.Accent, rstride=2, cstride=2, alpha=0.9, lw=0.75) ax.set_xlabel(u'X') ax.set_ylabel(u'Y') ax.set_zlabel(u'Z') plt.title(u'二元高斯分布,样本个数:%d' % d.shape[0], fontsize=20) plt.tight_layout(0.1) plt.show()




















 5万+
5万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








