一道关于最小生成树的傻逼题

最小生成树

题目描述

某个宇宙帝国有N个星球，由于宇宙的空间是三维的，因此每个星球的位置可以用三维坐标来表示（X, Y, Z）. 任意两个不同的星球i和j都有一条边相连，边的距离是这样计算的：dis[i,j] = min( |Xi－Xj|, |Yi－Yj|, |Zi－Zj|). 其中| |符号表示取绝对值。现在让你来挑N-1条边，让这N个星球连通成一个最小生成树，输出构成最小生成树的N-1条边的长度总和。

输入格式 1426.in

第一行，一个整数Ｎ。　1 <= N <= 100000
接下来有Ｎ行，每行三个整数: Ｘ,Ｙ,Ｚ。表示一个星球的坐标，-1000000000 <=Ｘ,Ｙ,Ｚ <= 1000000000.　没有两个星球的位置完全重叠。

输出格式 1426.out

一行，构成最小生成树的N-1条边的长度总和。

输入样例 1426.in

5
11 　-15 　-15
14　 -5 　-15
-1 　-1 　-5
10　 -4　 -1
19 　-4 　19

输出样例 1426.out

4

一看题目：便觉得这题很水。可一细看，发现边数是n*(n-1)/2条的，就不可以把所有的边排序。那么，先把问题简单化。

考虑一维的情况：不妨设所有的点为x1,x2……xn，且x1<x2<……<xn，则xi和x(i+1)|0<i<n之间连一条边是最优的。

如下图所示：我们发现，红色的方案的权值总和比绿色的多。

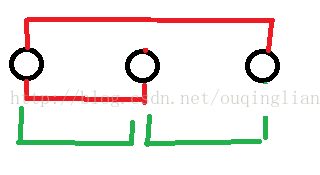
那么：我们可以把点按照x轴,y轴,z轴三个方向排序再把xi和x(i+1)连一条边。然后用Kruskal算法就可以了。时间复杂度为O(3nlog3n)。

转载于:https://www.cnblogs.com/ouqingliang/p/9245260.html