一、样本均值的分布
当总体为正态分布
X~N(μ,
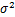 ),
),
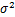 ),
),
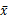 的抽样分布为正态分布,
的抽样分布为正态分布,
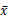 的期望为μ,方差为
的期望为μ,方差为
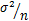 ,则
,则
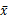 ~N(μ,
~N(μ,
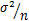 )
)
注:该方差为重复抽样时的方差(放回抽样),如果为不重复抽样,则方差为:
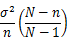
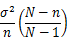
1、期望和方差
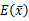 =μ
=μ
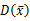 =
=
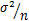
2、中心极限定理
如果X是任意分布形态的总体,E(x)=μ,D(x)=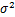
设从均值μ,方差为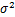 (有限)的任意一个总体中抽取样本量为n的样本,当n足够大时,样本均值
(有限)的任意一个总体中抽取样本量为n的样本,当n足够大时,样本均值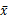 的抽样分布近似服从均值为μ,方差为
的抽样分布近似服从均值为μ,方差为 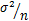
X~N(μ,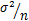 )
)
二、样本比例的抽样分布
在消费调查及民意检测中常要对具有某一特征的产品或事物的喜好人数进行研究,那是我们常假定总体中对具有某一特征产品的喜好比例为π,在此条件下去研究当从总体中随机抽取n个个体进行调查时,喜好某一个产品的人数X的概率。在实际应用中我们所关心的正好是总体喜好某一产品的人数的比例π,如果在样本大小为n的样本中具有某一特征的个体数为X,则样本比例用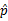 表示
表示
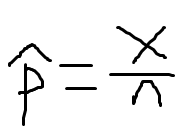
以后就用样本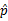 来估计总体比例π
来估计总体比例π
当n充分大是,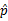 的分布可以用正态分布逼近,这有
的分布可以用正态分布逼近,这有

一般情况下,如果X是随机变量,C为一常数,则CX与X有相同的分布形状,设E(X)=μ,D(X)=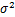 ,
,
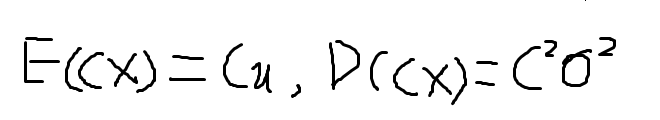
三、两个样本平均值之差的分布
设
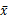 1是独立地抽自总体
X1~N(μ1,
1是独立地抽自总体
X1~N(μ1,
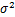 1
)的一个容量为n1的样本均值,
1
)的一个容量为n1的样本均值,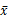 2
是独立地抽自总体
X2~N(μ2,
2
是独立地抽自总体
X2~N(μ2,
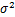 2
)的一个容量为n2的样本均值,则有
2
)的一个容量为n2的样本均值,则有
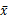 1是独立地抽自总体
X1~N(μ1,
1是独立地抽自总体
X1~N(μ1,
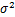 1
)的一个容量为n1的样本均值,
1
)的一个容量为n1的样本均值,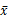 2
是独立地抽自总体
X2~N(μ2,
2
是独立地抽自总体
X2~N(μ2,
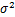 2
)的一个容量为n2的样本均值,则有
2
)的一个容量为n2的样本均值,则有
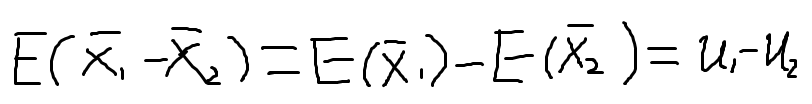
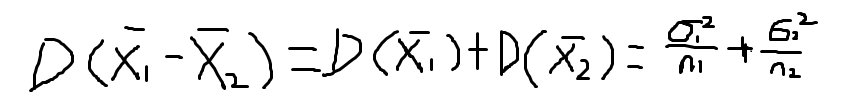
四、两个样本比例之差的抽样分布
设分别从具有参数π1和参数π2的二项总体中抽取包含n1个观测值和n2个观测值的独立样本,则两个样本比例差的抽样分布为:
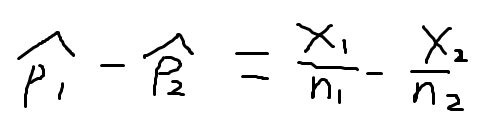
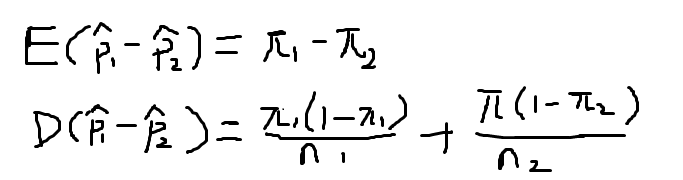
五、关于样本方差的分布
样本方差的分布
设X1,X2,...Xn为来自正态分布的样本,则可以推到出如下结果:设总体分布为
X~N(μ,
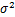 )的正态分布,则样本方差S^2的分布为:
)的正态分布,则样本方差S^2的分布为:
 )的正态分布,则样本方差S^2的分布为:
)的正态分布,则样本方差S^2的分布为:
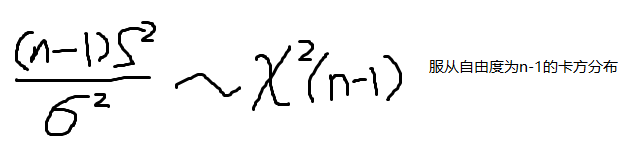
六、两个样本方差比的分布
设X1,X2,...,Xn1是来自正态总体N(μ1,
 1
)的样本,Y1,Y2,...Yn2是来自正态总体
N(μ2,
1
)的样本,Y1,Y2,...Yn2是来自正态总体
N(μ2,
 2
)的一个样本,且Xi(i=1,2,...,n1
)与Yi(i=1,2,...,n2)互相独立,则
2
)的一个样本,且Xi(i=1,2,...,n1
)与Yi(i=1,2,...,n2)互相独立,则
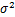 1
)的样本,Y1,Y2,...Yn2是来自正态总体
N(μ2,
1
)的样本,Y1,Y2,...Yn2是来自正态总体
N(μ2,
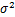 2
)的一个样本,且Xi(i=1,2,...,n1
)与Yi(i=1,2,...,n2)互相独立,则
2
)的一个样本,且Xi(i=1,2,...,n1
)与Yi(i=1,2,...,n2)互相独立,则
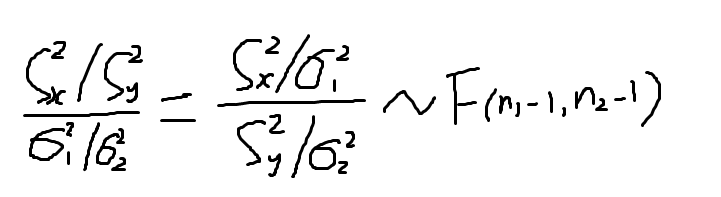
F(n1-1,n2-1)是第一自由度(分子自由度)为n1-1,第二自由度(分母自由度)为n2-1的F分布






















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








