数学不等式解析技巧-优快云博客

本文通过多个实例详细解析了数学不等式的解题方法，包括利用三角函数的有界性、数形结合思想解决直线与单位圆的问题，以及通过构造函数、做差法等方式比较表达式的大小。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

前言

典例剖析

例1【2017宝中训练题】若点$P(cos\theta，sin\theta)$在直线$\cfrac{x}{a}+\cfrac{y}{b}=1$上，则下列不等式正确的是（）。

A、$a^2+b^2\leq 1$ $\hspace{2cm}$ B、$a^2+b^2\ge 1$ $\hspace{2cm}$ C、$\cfrac{1}{a^2}+\cfrac{1}{b^2}\leq 1$ $\hspace{2cm}$ D、 $\cfrac{1}{a^2}+\cfrac{1}{b^2}\ge 1$

法1：三角函数的有界性，由于点$P(cos\theta，sin\theta)$在直线$\cfrac{x}{a}+\cfrac{y}{b}=1$上，则有$bcos\theta+asin\theta=ab$，即$\sqrt{a^2+b^2}sin(\theta+\phi)=ab，tan\phi=\cfrac{b}{a}$，由三角函数的有界性可知$|sin(\theta+\phi)|=|\cfrac{ab}{\sqrt{a^2+b^2}}|\leq 1$，即$\cfrac{\sqrt{a^2+b^2}}{|ab|}\ge 1$，即$\cfrac{1}{a^2}+\cfrac{1}{b^2}\ge 1$，故选D.

法2：数形结合，由已知可知点$P$在单位圆上，自己做出大致图像可知，直线和圆的位置关系只能是相切和相交，故圆心$(0，0)$到直线$bx+ay-ab=0$的距离应该小于等于半径1，即$\cfrac{|b\cdot 0+a\cdot 0-ab|}{\sqrt{a^2+b^2}}\leq 1$，化简得$\cfrac{1}{a^2}+\cfrac{1}{b^2}\ge 1$，故选D.

例2$a>b>1$是$a+\cfrac{1}{a}>b+\cfrac{1}{b}$的(充分不必要)条件。

法1：常规用做差法，由已知可知$ab-1>0，a-b>0$，$a+\cfrac{1}{a}-b-\cfrac{1}{b}=a-b-\cfrac{a-b}{ab}=(a-b)\cfrac{ab-1}{ab}>0$，即$a+\cfrac{1}{a}>b+\cfrac{1}{b}$，故充分性成立；当$a=\cfrac{1}{4}，b=\cfrac{1}{2}$时，满足$a+\cfrac{1}{a}>b+\cfrac{1}{b}$，但不能得到$a>b>1$，故必要性不成立。

法2：巧解构造函数法，令$f(x)=x+\cfrac{1}{x}$，则原题目变形为$a>b>1$是$f(a)>f(b)$的什么条件，结合对勾函数的图像很容易判断。

例3已知$x^2+y^2\leq 1$，求$|2x+y-2|+|x+3y-6|$的最小值？

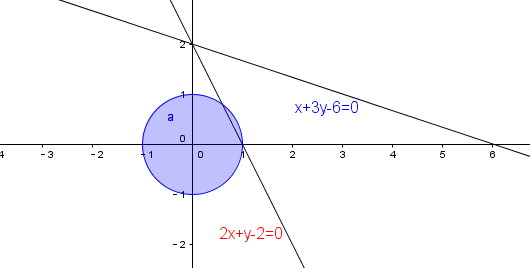
思路一：从形入手思考，转化为点线距；

我们发现$|2x+y-2|+|x+3y-6|=\sqrt{5}\cfrac{|2x+y-2|}{\sqrt{5}}+\sqrt{10}\cfrac{|x+3y-6|}{\sqrt{10}}$，

其中表达式$\cfrac{|2x+y-2|}{\sqrt{5}}$和$\cfrac{|x+3y-6|}{\sqrt{10}}$分别表示圆内及圆上的动点

到两条直线的距离，所以可以把“数”的问题转化为“形”的问题。

思路二：三角代换，令$x=R\cos\theta，y=R\sin\theta，R\in[0，1]$，

则$|2x+y-2|+|x+3y-6|\ge|3R\cos\theta+4R\sin\theta-8|=|5R\sin(\theta+\phi)-8|$

例4【分子有理化、分母有理化】

已知$a=\sqrt{2}$，$b=\sqrt{7}-\sqrt{3}$，$c=\sqrt{6}-\sqrt{2}$，比较$a、b、c$的大小。

分析：$b=\sqrt{7}-\sqrt{3}=\cfrac{\sqrt{7}-\sqrt{3}}{1}=\cfrac{4}{\sqrt{7}+\sqrt{3}}$；

$c=\sqrt{6}-\sqrt{2}=\cfrac{\sqrt{6}-\sqrt{2}}{1}=\cfrac{4}{\sqrt{6}+\sqrt{2}}$；

由于$\sqrt{7}+\sqrt{3}>\sqrt{6}+\sqrt{2}$，故$\cfrac{4}{\sqrt{7}+\sqrt{3}}<\cfrac{4}{\sqrt{6}+\sqrt{2}}$，

即$b<c$，

又$\sqrt{2}(\sqrt{6}+\sqrt{2})=2\sqrt{3}+2>4$，故$\sqrt{2}>\cfrac{4}{\sqrt{6}+\sqrt{2}}$，

即$c<a$，故$b<c<a$；

例5【用不等式性质求范围】

①已知$1<\alpha<3$，$-4<\beta<2$，求$\alpha-|\beta|$的取值范围。

分析：由于$-4<\beta<2$，

则$0\leq |\beta|<4$，即$-4<-|\beta|\leq 0$，

又$1<\alpha<3$，同向不等式相加，得到

$-3<\alpha-|\beta|<3$，注意，右端等号不能同时取到，

故$\alpha-|\beta|\in (-3，3)$。

②已知$-\cfrac{\pi}{2}<\alpha<\beta<\cfrac{\pi}{2}$，求$\alpha-\beta$的取值范围；

分析：①已知条件等价转化为不等式组$\left\{\begin{array}{l}{-\cfrac{\pi}{2}<\alpha<\cfrac{\pi}{2} }\\\\{ -\cfrac{\pi}{2}<\beta<\cfrac{\pi}{2} }\\\\{ \alpha<\beta }\end{array}\right.$，

这样得到$-\pi<\alpha-\beta<\pi$，且$\alpha-\beta<0$，故$-\pi<\alpha-\beta<0$，

③已知$-\cfrac{\pi}{2}<\alpha<\beta<\cfrac{\pi}{2}$，求$2\alpha-\beta$的取值范围；

分析：仿上，先转化得到$-\pi<\alpha-\beta<0$，又由于$-\cfrac{\pi}{2}<\alpha<\cfrac{\pi}{2}$，

两个同向不等式相加，得到$-\cfrac{3\pi}{2}<2\alpha-\beta<\cfrac{\pi}{2}$，

例6【比较大小】若$P=\sqrt{a+2}+\sqrt{a+5}$，$Q=\sqrt{a+3}+\sqrt{a+4}(a\ge 0)$，比较$P、Q$的大小。

分析：由于$a\ge 0$，$P > 0$，$Q > 0$，

则有$Q^2-P^2=2a+7+2\sqrt{a^2+7a+12}-(2a+7+2\sqrt{a^2+7a+10})$

$=2(\sqrt{a^2+7a+12}-\sqrt{a^2+7a+10}) > 0$，

所以$Q^2 > P^2$，则$Q > P$。

例7【比较大小】【2019高三理科数学启动卷，2019陕西省二检试卷第5题】若正实数$a$，$b$满足$a>b$，且$lna\cdot lnb>0$，则

$A.\cfrac{1}{a} > \cfrac{1}{b}$ $B.a^2 < b^2$ $C.ab+1 > a+b$ $D.lga+lgb > 0$

分析：由于$a>b>0$，则得到$\cfrac{1}{a}<\cfrac{1}{b}$，且$a^2>b^2$，故选项$A$，$B$错误；