旅行商问题

     旅行商问题（Traveling Saleman Problem，TSP）又译为旅行推销员问题、货郎担问题，简称为TSP问题，是最基本的路线问题，该问题是在寻求单一旅行者由起点出发，通过所有给定的需求点之后，最后再回到原点的最小路径成本。最早的旅行商问题的数学规划是由Dantzig（1959）等人提出。

• 问题描述

由n个城市组成的网络，编号为V1,V2,....,Vn, Dij 表示Vi到Vj的距离(或时间，费用等)，一般Dij ≠ Dji，一个推销员从V1开始，访问每个城市一次且仅一次，然后返回V1。这个推销员如何选择线路，才能使行程最短？

• 问题抽象

一个有向图G(V,E)，从某个顶点出发，经过每个结点一次且仅一次，返回出发结点。对于任意Vi,Vj ∈ V , 存在Eij和Eji，0 < Eij < ∞ ，0 < Eji < ∞，如果没有此条件，问题有可能无解，也就是说，此图是一个有向完全图。

• 问题求解

(1)枚举法

相当于对V1,V2,V3,....,Vn做圆周排列，圆周排列为n!/n = (n-1)!，也即有(n-1)!条路径，需要(n-1)(n-1)!次加法，(n-1)!-1次比较。

(2)动态规划

令f(Vi ; V)表示结点从结点Vi出发，遍历V中的点一次且仅一次，然后返回V1的最短距离，其中V是某些结点构成的集合，且V1,Vi 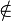 V。

多段判决公式： f(Vi ; V ) = min { Dij + f(Vj ; V\{Vj} }  (Vj ∈ V)

因此问题就成了求 f(V1 ; { V2,V3,V4,...,Vn} } 的最小值

本文转自nxlhero 51CTO博客，原文链接：http://blog.51cto.com/nxlhero/696905，如需转载请自行联系原作者