《中国人工智能学会通讯》——11.19 动态多任务学习机制

11.19 动态多任务学习机制

上两节提出了两种学习交通路网中任务复杂关系的多任务学习模型。上述的多任务学习方法假设数据是静态的，且数据中所蕴含的任务关系以及任务与特征间的关系恒定不变。而在交通问题中，这些关系随着时间会产生变化，因此体现出复杂的动态关系模式。例如，在每天的交通模式中，早、午、晚以及凌晨的交通流中所蕴含的模式各不相同，并随时间在不断变化。本节将对 CRMTL 模型和 THMTL 模型中提出的多任务学习方法进行扩展，使其适用于动态数据环境。由于动态性的扩展原理对 CRMTL 模型和 THMTL 模型相同，下面以THMTL 为例进行阐述，CRMTL 的动态扩展可以类似进行。

假设 t = 1,2,···,L 为数据中的不同时刻，第 i 个任务在 t 时刻的数据为 。当 t 变化时，学习任务间动态的关系，以及任务与特征间动态的关系十分困难。处理动态数据最为直观的方法便是对任意时刻 t 均建立多任务模型，将时变问题拆分为单独时刻的静态问题。这样的做法简单，但常常伴随而来的问题是不稳定的学习结果。这种不稳定性是指当单独对不同时刻进行多任务建模时，学习出的结果在相邻时刻的波动性很大。例如，在交通问题中，早 9:00-9:15 与 9:15-9:30 时段的交通规律应当具有很强的相似性，这称之为交通系统的动态连续性。而在如此邻近的时刻，如果学习的结果截然不同，便会对时序的交通分析带来很大的误差。造成上述现象的原因通常为数据中所隐含的波动性，以及模型的不稳定性。因此，减少时变数据中的波动，以及增强多任务模型的稳定性是解决动态多任务建模问题的关键。为实现上述目的，本节利用交通时间上的连续性特点对模型进行如下处理。

在 CRMTL 与 THMTL 模型的求解中，使用到的梯度项 (W) 的每一列为 ，可知在模型求解过程中所涉及到的与数据相关的项为和 。由原文中的算法时间复杂度的分析得知， 和 均可在算法运行前进行预计算并存储起来。事实上，当数据进行规则化之后， 即为X i 的协方差矩阵， 代表了 X i 中的每个特征与输出 y i 之间的相关性。假设动态数据实时地到来，当前时刻为 t，将第 i 个任务所涉及的数据相关项进行如下转换 :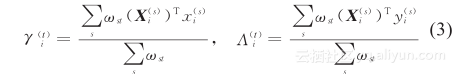
其中 ω st 为 s 时刻与 t 时刻间的相似性权重。ω st 定义为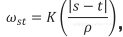其中，K(·) 为核函数，例如常用的高斯核函数，K(x) = exp (-x 2 )；ρ 为用于控制时间差值的尺度系数；s 为与 t 相邻近的时刻，假定在 Lag 时长的范围内，相邻的时刻间都存在连续性关系，则 s=t,t-1,···,t-Lag。式 (3) 利用了时间上的连续性对当前时刻 t 及其邻近时刻的数据进行了加权平均，其优点是消除了动态数据中所含有的波动。以 THMTL 模型为例，将式 (3) 作为 t 时刻第 i个任务的相关数据项代入式 (2)，则动态的多任务层次结构学习方法 (Dynamic THMTL, DTHMTL)在 t 时刻的求解算法中，梯度项 的每一列为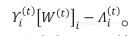由于 DTHMTL 模型与式 (2) 的基本形式相同，其区别在于式 (3) 采用的动态性处理方法，因此 DTHMTL 模型可以使用类似算法进行求解。详情请参看全文。