matlab中一组数取百分位数_GRE数学难题-正态分布+百分位数

1 基本概念

在图标题中考察正态分布和百分位数时，通常会涉及以下基本概念

算术平均值(arithmetic) = 平均值(average) = 均值(mean) - 容易受极值影响

加权平均数 = Σ（权重 * 数值） / Σ 权重 - 容易受极值影响

权重 = 出现次数 = 频率

中位数(median) - 不容易受极值影响

计算n个数字的中位数时,先将数字从小到大进行排序得到一个有序数列。

如果n是奇数,中位数就是有序数列最中间的那个数。

如果n是偶数,最中间便有两个数。中位数就是这两个数的平均数

指在这组数据中出现次数最多的那个数

四分位数和百分位数

用L指代最小的数,G指代最大的数M指代中位数。

一组数据中最常见的位置是四分位数和百分位数

可以将一组从小到大排列好的数据分成若干个大致相同的部分。

一组数据中有3个四分位数把这组数据分为4个部分,

有99个百分位这组数据分成100个大致相同的部分

和平均数、中位数一样,四分位数和百分位数可能不是该组数据中出现的值

3个4分位数依次为Q1，Q2，Q3

则Q2 = M

99个100分位数依次为P1，... P50，... P99

M=Q2=P50

四分位数距( interquartile range)

第一个四分位数和第三个四分位数之间的差值,即Q3 - Q1

极差(range) = max-min

标准差( standard deviation)

与极差和四分位距有所不同,标准差(standard deviation)与一组数据中每个数据都有联系。

数据偏离平均值越远,标准差就越大

数据越集中在平均值附近,标准差就越小

n个数据的标准差：

(1)计算n个值的平均值

n'

(2)计算每个数据与平均值的差

d1 = n1 - n',

d2 = n2 - n',

...

dn = n - n'

(3)标准差=（(d1^2+ d2^2 + ...+dn^2) /n）^(0.5)

样本标准差(sample standard deviation) = 总体标准差(population standard deviation)

=（(d1^2+ d2^2 + ...+dn^2) /(n-1)）^(0.5)

频率直方图 / 柱状图

如果柱状图每个柱子的底宽为1，则柱状图中代表相对频率的条形面积之和为1。

尽管柱状图横轴上的单位会有变化,我们可以调整纵轴的单位使得条形面积总和为1。

这其实可以说是正态分布图的本质，理解这一点对于做正态分布的题非常关键

一组数据的平均值、中位数、偏离平均值整数倍标准差的数值 须在横轴上标记

通过这些标记我们能够看出是否大多数的数据落在偏离平均值标准差*3的区间内,

即在区间(m-3d,m+3d)内，其中d为标准差

在柱状图（频率分布直方图）中,可观察出如下数据

众数：最高矩形的底边中点的横坐标

算术平均数：每组数值的中间值乘以频率后相加

中位数：把频率分布直方图分成两个面积相等部分的平行于Y轴的直线横坐标

2 怎么理解随机变量-中位数

随机变量X的概率分布

下面这个表格作出了X的6个可能的值以及其对应可能出现的概率,

这个表叫作随机变量X的概率分布(probability distribution)

X的平均数或者期望M（x）=x*P(x)

X P（x）

0 12%

1 20%

2 27%

3 25%

4 16%

其实如果我们假设X总共出现了100次，那么这个表的本质其实是这样：

0，0, 0，... 0 ，1, 1, ... ,1,1, 1，2,2 ... 2,2,2，3,3, ... ,3,3,3，4,4 ... 4,4,4

|--- 12个----| | --- 20个---| |--- 27个---| |--- 25个---| |--- 16个---|

即一堆数字从小往大排列，0连续出现了12次，1连续出现了20次等

所以如果你遇到一个有题目给了你一张这样的表格，问你中位数是多少，

那么你只要求第50个数落在哪个区间里即可

由于12+20=32，而32+27=59，所以第50个数必然落在2这个区间里

所以中位数=2

如果你理解了这一点，其实正态分布图就是把这个表画成图而已，

这张图和百分位数/四分位数/中位数/众数的关系，其实就是我刚刚讲的这样

3 正态分布( Normal Distribution) + 百分位数/四分位数/中位数/众数

近似正态分布(approximately normally distributed)

正态分布(normal distribution)

这条曲线下方的区域代表连续概率分布

连续概率分布有许多不同的类型,其中最重要的是正态分布

在分布曲线下的部分面积为1

在分布曲线下的部分面积为1

这样一个随机变量叫作连续随机变量,

它与代表从数据分布中随机取值的随机变量扮演着同样的角色

不同的是,我们很少把连续随机变量中的事件看成一个单一的值,比如X=3。

我们通常把事件描述成一个区间内的值,比如1<X<3或者X>10

如果某个数是数列中的第n个数字，

那么它在正态分布图形里从左端点开始围合成的面积也为n

正态分布的内涵：

横轴表示的连续随机变量（从左往右连续单调递增）

纵轴表示的是横轴的某个值（当x等于横轴某个值时）出现的次数

n分位数在正态分布图上的意义是面积等分n份的99个分界线（n通常为4，100）

随机变量x的值（value）在图上的意义是x坐标轴

比如一组数0，1，2，4，4，4，6，7，8 中位数是4

那么中位数4对应的纵轴会是3，因为出现了3次

其实正态分布就是这种数列的简单表示方法

就是不需要逐个列出重复的数字，而是用重复的次数来表示即：

0，1，2，4，4，4，6，7，8

-->

0，1，2，4，6，7，8（横轴）

1，1，1，3，1，1，1（纵轴）

但要注意，上面这个例子只是在说明横纵轴的关系

但不能表示x轴的特点

正太分布的横轴是连续变化的值

即和普通的平面直角坐标系一样，x是从左往右连续单调递增的实数集

---

例题

170-17. The random variable X is normally distributed. The values 650 and 850 are at the 60th and 90th percentiles of the distribution of X, respectively.

Quantity A: The value at the 75th percentile of the distribution of X

Quantity B: 750

A. Quantity A is greater.

B. Quantity B is greater.

C. The two quantities are equal.

D. The relationship cannot be determined from the information given.

首先百分位数意味着把一组数分成100分，所以一共有99个百分位数，

类似于用99个点把一条线段分成了100份，

每份包含的数据个数相同

那么50th百分位数肯定就是中位数：（1+99）/ 2=50

50th到60th，90th到最末的数字个数肯定是一样的，都是m个（m=n/100）

这是百分位数的定义决定的

但由于这个是正态分布，数字个数在图上的几何意义不是x值，而是面积

所以在下图中，60th在x轴上的位置一定会更靠左，90th则更靠右

两个阴影部分面积相等：均为m

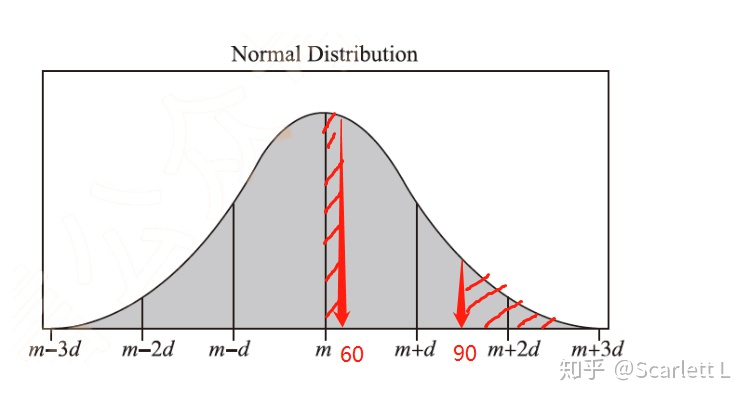
然后我们来看75th

首先，75th是60th（650）到90th（850）的中间值

同理，虽然75=（60+90）/2，

但是由于正态分布的特点，75th肯定更接近60th

也就是说75th的值会更接近650，所以是A

这里在做题的时候可能有人会觉得，就算75th更接近650

题干也没给出数值分布，也没给出每一份到底有多少个数

为什么不能是我从650直接跳到750，

那就算75th接近650，它还是可以是750，甚至更大

这是因为正态分布是连续变量

即每个横坐标的数值都是均匀变化的，只不过是出现的次数不均匀而已

所以x的取值就是连续分布均匀递增的，其实就和任何一个平面直角坐标系的x轴一样

其实正态分布是从这种条形图演变过来的，

可以看到每个柱子的宽度是相等而且连续的

也就是说肯定是每n个一组，然后从( 0,n-1)，(n,2n-1)这样一直下去

而不会出现2n，6n，7n这种情况

所以从650-850其实在x上一定是均匀变化的

问题是在于百分位数是把重复的数字都列了出来，所以百分位数在x轴上的分布不均匀

如图所示

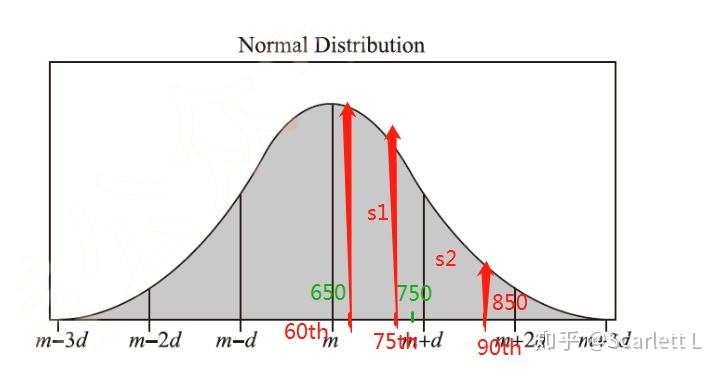
750一定在650和850的正中，所以其实也在60th和90th的正中

但75th百分位数在哪里，其实是要看面积大小（其实就是要考虑同一个x出现了多次）

而在60th附近y值明显更高，所以要让s1=s2，75th的横坐标必然要从中间往左偏

所以75th的横坐标必然小于750，即它的x值、它的value小于750

---

例278:

调查了5500人一年每人读书的数量,满足正态分布,其中 with mean等于19本, standard deviation等于2。问读书最多的880个人每年至少读多少本书?

根据上图，书为横轴，人数为纵轴

图形面积为总人数，即5500

读书最多的人即横轴最大的这部分，即最靠右的这部分

880/5500=16%

根据正态分布的特性，2/3的人偏离1个方差，那么从m+d到m+3d的面积就是（1-2/3）/2=1/6=16.7%>16%

所以应该是往m+d右边再偏一点点，所以至少是m+d=21本书

170-61

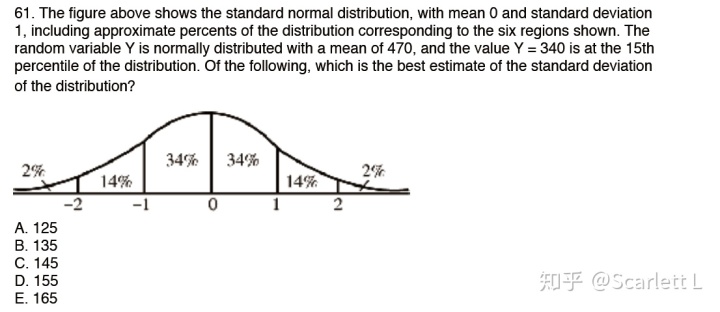
如果某个数是数列中的第n个数字，

那么它在正态分布图形里从左端点开始围合成的面积也为n

所以15 / （50-15） = 51/119 < 16%/34% = 56/119

所以15th会出现在m-d左边一点点，即15th < m-d

所以m-d = 470-d > 340

--> d < 470-340=130

所以是A

总结：

1 正态分布横轴表征的是连续递增的数，纵轴表征的是各个数出现的频率（做题的时候可以理解为次数）

2 四分位数/百分位数/中位数对应的是正态分布相应图形面积的分界线所对应的的横坐标数值

如Q1代表的是：

从图形最左边到某一条平行于y轴的线围成的面积S，且S恰好是整个图形面积的1/4，那么这条线对应的x值就是Q1