数独终盘生成算法解析-优快云博客

本文介绍了数独终盘的生成方法，包括矩阵转换法（数字交换、行或列调整）和随机法。矩阵转换法通过种子矩阵变换产生新终盘，随机法则通过随机填充数组来生成，讨论了其概率有效性。这两种方法提供了创建数独终盘的不同思路。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

2019独角兽企业重金招聘Python工程师标准>>>

数独（すうどく，Sudoku）是一种运用纸、笔进行演算的逻辑游戏。玩家需要根据9×9盘面上的已知数字，推理出所有剩余空格的数字，并满足每一行、每一列、每一个粗线宫内的数字均含1-9，不重复。

一般情况下，产生一个数独题目，包含两个步骤：

产生一个数独终盘（9X9）

在第一步产生的数独终盘中，根据难易程度，在终盘上挖掉不同数目的数字。

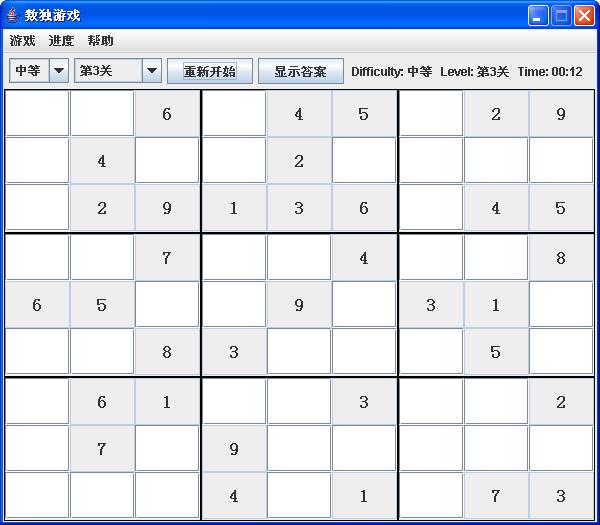
经过该两个步骤之后，我们就可以将某一个数独难题展示出来，如：

本文列举数独终盘产生的几个方法，大家一起来看看吧。

矩阵转换法

矩阵转换法，简言之，就是对一个已有的数独终盘矩阵进行操作。

主要采用交换数字、交换行/列数据等方法，产生新的矩阵。

为了完成矩阵的转换，我们需要有可用的数独终盘矩阵作为种子矩阵才行。可以采用如下做法完成：

先给定几个可用数独终盘作为备选种子矩阵。

产生一个随机数，随机选中其中的一个作为种子矩阵。

如编写一个产生种子矩阵的工具类：

import java.util.Random;

/**
 * 
 * @author wangmengjun
 *
 */
public final class SeedSudokuMatrixFactory {

	private static final int seedSudokuArrays[][][] = {
			{ { 1, 2, 3, 4, 5, 6, 7, 8, 9 }, { 4, 5, 6, 7, 8, 9, 1, 2, 3 },
					{ 7, 8, 9, 1, 2, 3, 4, 5, 6 },
					{ 2, 1, 4, 3, 6, 5, 8, 9, 7 },
					{ 3, 6, 5, 8, 9, 7, 2, 1, 4 },
					{ 8, 9, 7, 2, 1, 4, 3, 6, 5 },
					{ 5, 3, 1, 6, 4, 2, 9, 7, 8 },
					{ 6, 4, 2, 9, 7, 8, 5, 3, 1 },
					{ 9, 7, 8, 5, 3, 1, 6, 4, 2 } },
			{ { 3, 9, 4, 5, 1, 7, 6, 2, 8 }, { 5, 1, 7, 6, 2, 8, 3, 9, 4 },
					{ 6, 2, 8, 3, 9, 4, 5, 1, 7 },
					{ 9, 3, 5, 4, 7, 1, 2, 8, 6 },
					{ 4, 7, 1, 2, 8, 6, 9, 3, 5 },
					{ 2, 8, 6, 9, 3, 5, 4, 7, 1 },
					{ 1, 4, 3, 7, 5, 9, 8, 6, 2 },
					{ 7, 5, 9, 8, 6, 2, 1, 4, 3 },
					{ 8, 6, 2, 1, 4, 3, 7, 5, 9 } },
			{ { 7, 6, 1, 9, 8, 4, 2, 3, 5 }, { 9, 8, 4, 2, 3, 5, 7, 6, 1 },
					{ 2, 3, 5, 7, 6, 1, 9, 8, 4 },
					{ 6, 7, 9, 1, 4, 8, 3, 5, 2 },
					{ 1, 4, 8, 3, 5, 2, 6, 7, 9 },
					{ 3, 5, 2, 6, 7, 9, 1, 4, 8 },
					{ 8, 1, 7, 4, 9, 6, 5, 2, 3 },
					{ 4, 9, 6, 5, 2, 3, 8, 1, 7 },
					{ 5, 2, 3, 8, 1, 7, 4, 9, 6 } },
			{ { 7, 1, 5, 4, 3, 6, 2, 9, 8 }, { 4, 3, 6, 2, 9, 8, 7, 1, 5 },
					{ 2, 9, 8, 7, 1, 5, 4, 3, 6 },
					{ 1, 7, 4, 5, 6, 3, 9, 8, 2 },
					{ 5, 6, 3, 9, 8, 2, 1, 7, 4 },
					{ 9, 8, 2, 1, 7, 4, 5, 6, 3 },
					{ 3, 5, 7, 6, 4, 1, 8, 2, 9 },
					{ 6, 4, 1, 8, 2, 9, 3, 5, 7 },
					{ 8, 2, 9, 3, 5, 7, 6, 4, 1 } } };

	private SeedSudokuMatrixFactory() {
	}

	/**
	 * 随机获取一个预先定义好的数独数组
	 */
	public static int[][] retrieveSeedSudokuArrayByRandom() {
		int randomInt = new Random().nextInt(seedSudokuArrays.length);
		return seedSudokuArrays[randomInt].clone();
	}
}

有了种子矩阵之后，我们就可以对某个种子矩阵做矩阵转换处理，从而获取更多的可用的数独终盘矩阵。

两个数互相交换法

下图就是一个数字9和数据1交换的例子：

import java.util.Arrays;
import java.util.Collections;
import java.util.List;

/**
 * 
 * @author wangmengjun
 *
 */
public class SudokuPuzzleMatrixGenerator {

	/** 待转换的数组种子数组 */
	private int[][] sampleArray = SeedSudokuMatrixFactory
			.retrieveSeedSudokuArrayByRandom();

	public int[][] generateSudokuArray() {
		List<Integer> randomList = buildRandomList();
		for (int i = 0; i < 9; i++) {
			for (int j = 0; j < 9; j++) {
				for (int k = 0; k < 9; k++) {
					if (sampleArray[i][j] == randomList.get(k)) {
						sampleArray[i][j] = randomList.get((k + 1) % 9);
						break;
					}
				}
			}
		}
		return sampleArray;
	}

	private List<Integer> buildRandomList() {
		List<Integer> result = Arrays.asList(