二叉查找树

二叉查找树详解

最新推荐文章于 2025-09-11 18:44:42 发布

weixin_33816611

最新推荐文章于 2025-09-11 18:44:42 发布

阅读量64

点赞数

CC 4.0 BY-SA版权

文章标签：数据结构与算法

原文链接：http://www.cnblogs.com/KennyRom/p/6080998.html

本文详细介绍了二叉查找树的概念及其构建方法，包括插入、查找和删除操作的具体实现过程。

1、什么是二叉查找树

二叉查找树就是空树或者是每一个结点都有作为查找的依据，并且所有的做左子树的依据都比根结点的小，所有右子树的依据都比根结点的小

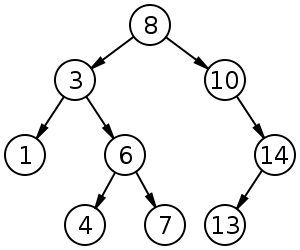
这就是一棵二叉查找树

同时我们可以看到假如对一棵这样的树进行中序遍历时，可以发现所有依据都将按照从小到大排名

中序遍历：1 3 4 6 7 8 10 13 14

同时我们也可以看到最左的结点的依据是最小的，最右的结点是最大的

2、如何构建？

1）数据类型

其实就是二叉树加上个依据而已

typedef struct {int key;} ElemType;
typedef struct BitTNode
{
	ElemType data;
	struct BitTNode *lchild, *rchild;
}BitTNode, *BitTree;

2)如何构建呢？

从空树出发，依次插入数据

（1）如果是空树则插入结点就是二叉查找树的根结点

（2）如果非空，则插入值与根结点比较，若小于根结点则进入左子树，若大于则进入右子树，递归比较。

对于一棵二叉查找树最重要的是查找，查找就是按照二叉树的定义查找

有了查找算法后我们可以定义插入算法，有以结点方式插入，有以依据方式插入

// Insert node
void Insert_BitTree_1(BitTree &T, BitTree S)
{
   BitTree p; //use to find the place to insert
   BitTree q; //use to store the parent

   if(!T) T=S;  //空树直接插入
   else
   {
   	p=T;
   	while(p)
   	{
   		q=p;    //记录父母
   		if(S->data.key < p->data.key)
   		{
   			p=p->lchild;
   		}
   		else p=p->rchild;
   	}
   	if(S->data.key < q->data.key)
   		q->lchild = S;
   	else
   		q->rchild = S;
   }
}

// Insert node
void Insert_BitTree_2(BitTree &T, int key)
{
	BItTree p;
	BitTree q;
    BitTree S = new BitTNode();

	if(!T)      //空结点
	{
		S->data.key = key;
		S->lchild = NULL;
		S->rchild = NULL;
		T=S;
	}
	else
	{
		p = T;
		while(p)
		{
			q=p;
			if(key > p->data.key)
			{
				p=p->rchild;
			}
			else p=p->lchild;
		}
		if(q->data.key < key)
        {
        	S->data = key;
		    S->lchild = NULL;
		    S->rchild = NULL;
            q->rchild = S;
        }
        else
        {
            S->data.key = key;
		    S->lchild = NULL;
		    S->rchild = NULL;
            q->lchild = S;	
        }
	}
}

有插入之后我们需要删除

删除二叉查找树有两种情况

一、删除叶子结点

直接删除

二、删除根结点

（1）如果有两个孩子

选择根结点的左子树中最大的结点作为新的根结点

或者选择根结点的右子树最小的结点作为新的根结点

（2）如果只有一个孩子

则直接把他的孩子作为根结点

void Delete_BST(BitTree &T, int key)
{
	BitTree p, f;
	p = T;      //p为要删除的结点
	f = NULL;   //用f储存要删除的结点的父母
	while(p)
	{
		if(p->data.key == key)
		{
			delNode(T, p ,f);      // 找到要删除的结点，传入删除函数进行删除
		}
		else if(p->data.key < key)
		{
			f=p;
			p=p->rchild;
		}
		else if(p->data.key>key)
		{
			f=p;
			p=p->lchild;
		}
	}
}

void delNode(BitTree &T, BitTree p, BitTree f)
{
	BitTree s, q;   //用s储存要删除的结点的孩子结点
	int tag;
	tag=0;

	if(!p->lchild) s=p->rchild;  //没有左孩子则记录右孩子
	else if(!p->rchild) s=p->lchild;  //没有右孩子则记录左孩子
	else   // 有两个孩子
	{
       //要找左子树中最大的结点做根
		q=p;
		s=p->lchild;
		while(s->rchild)
		{
			q=s;        //s储存要做根的结点，q储存s的父母
			s=s->rchild;
		}
		p->data=s->data;
		if(q==p)q->lchild=s->lchild;
		else q->rchild=s->lchild;
		delete s;
		tag=1;
	}
	if(!tag)   //有1个孩子
	{
        if(!f)T=s;    //删除的是根结点
        else if(f->lchild==p)f->lchild=s;
        else f->rchild=s;
        delete p;
	}
}

转载于:https://www.cnblogs.com/KennyRom/p/6080998.html