CS 229 notes Supervised Learning
标签(空格分隔): 监督学习 线性代数
Forword
the proof of Normal equation and, before that, some linear algebra equations, which will be used in the proof.
The normal equation
Linear algebra preparation
For two matrices and
such that
is square,
.
Proof:
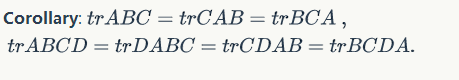
Some properties:
some facts of matrix derivative:
Proof:
Proof 1:
Proof 2:
Proof:
(refers to the cofactor)
Least squares revisited
(if we don’t include the intercept term)
since ,

Thus,
$\frac{1}{2}(X\theta-\vec{y})^T(X\theta-\vec{y}) =
\frac{1}{2}\displaystyle{\sum{i=1}^{m}(h\theta(x^{(i)}) -y^{(i)})^2} = J(\theta) $.
Combine Equations :
Hence
Notice it is a real number, or you can see it as a matrix, so
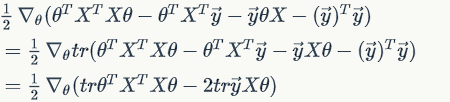
since and
involves no
elements.
then use equation with
,

To minmize , we set its derivative to zero, and obtain the normal equation:




 本文探讨了监督学习中正规方程的证明过程,并回顾了最小二乘法的相关概念。文章首先介绍了所需的线性代数预备知识,接着详细推导了正规方程,并通过矩阵微分进一步解释了其原理。
本文探讨了监督学习中正规方程的证明过程,并回顾了最小二乘法的相关概念。文章首先介绍了所需的线性代数预备知识,接着详细推导了正规方程,并通过矩阵微分进一步解释了其原理。
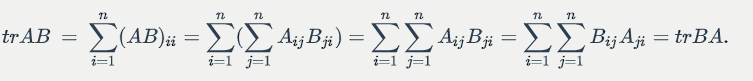
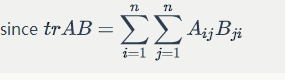
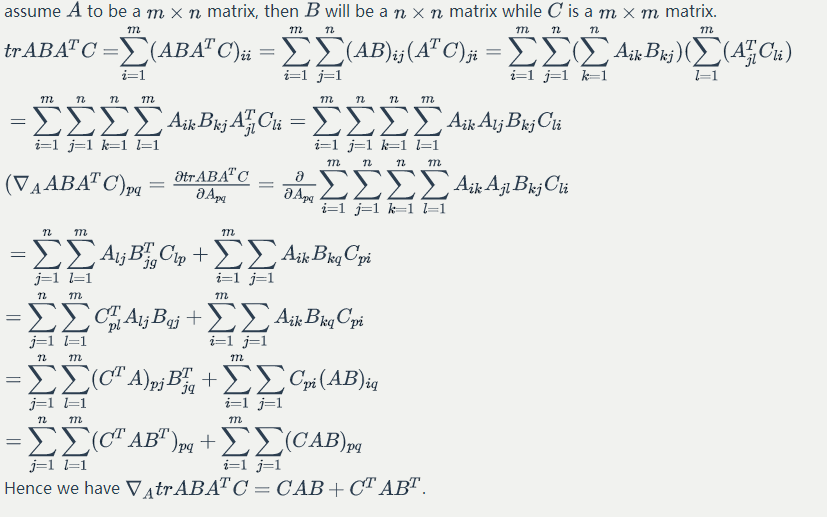

















 294
294

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








