数据结构5.4_m元多项式的表示

 

三元多项式表示如下：

P(x,y,z) = x¹⁰y³z² + 2x⁶y³z² + 3x⁵y²z² + x⁴y⁴z + 6x³y⁴z + 2yz + 15

然后对式子进行变形：

P(x,y,z)=((x¹⁰+2x⁶)y³+3x⁵y²)z²+((x⁴+6x³)y⁴+2y)z+15

上面的三元多项式可以看成是z的一元多项式。即P(x,y,z)=Az²+Bz¹+Cz⁰

其中A=((x¹⁰+2x⁶)y³+3x⁵y²)、B=((x⁴+6x³)y⁴+2y)、C=15；

然后二元多项式A(x,y)又可以看成是关于y的一元多项式；B也如此；

A(x,y)=((x¹⁰+2x⁶)y³+3x⁵y²)=Cy³+Dy²

其中C=x¹⁰+2x⁶、D=3x⁵、

分解到此处可以看出C、D是关于x的一元多项式；

这种嵌套结构把m元多项式层层分解；很好地表示了一元多项式。

 

任何一个m元多项式可以分解出一个主变元，随后再分解出第二个变元等等；

 接下来可以用广义表的数据结构来表示m元多项式；

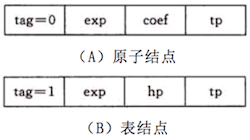
1 typedef struct MPNode{
2         ElemTag    tag;  //区分原子节点or
3         int             exp;  //指数域  
4         union{
5                 float    coef;  //指向系数域
6                struct   MPNode   *hp;  //表节点的表头指针
7         };
8         struct MPNode    *tp; //相当于线性链表的next，指向下一个元素的结点
9 }* MPList;

 

相关链接：

数据结构28：广义表及m元多项式：https://www.cnblogs.com/ciyeer/p/9040516.html

转载于:https://www.cnblogs.com/grooovvve/p/10398311.html