poj——3687 Labeling Balls

　　　　　　　　　　　　　　　　　　　　Labeling Balls

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 14835		Accepted: 4346

Description

Windy has N balls of distinct weights from 1 unit to N units. Now he tries to label them with 1 to N in such a way that:

1. No two balls share the same label.
2. The labeling satisfies several constrains like "The ball labeled with a is lighter than the one labeled with b".

Can you help windy to find a solution?

Input

The first line of input is the number of test case. The first line of each test case contains two integers, N (1 ≤ N ≤ 200) and M (0 ≤ M ≤ 40,000). The next M line each contain two integers a and b indicating the ball labeled with a must be lighter than the one labeled with b. (1 ≤ a, b ≤ N) There is a blank line before each test case.

Output

For each test case output on a single line the balls' weights from label 1 to label N. If several solutions exist, you should output the one with the smallest weight for label 1, then with the smallest weight for label 2, then with the smallest weight for label 3 and so on... If no solution exists, output -1 instead.

Sample Input

5

4 0

4 1
1 1

4 2
1 2
2 1

4 1
2 1

4 1
3 2

Sample Output

1 2 3 4
-1
-1
2 1 3 4
1 3 2 4

题意：
有T组测试数据，每组测试数据第一行有两个数n，m。代表有n个球，接下来m行，每行有两个数a，b，代表a球比b球轻，让你从小到大输出球的重量，若是相同重量，按照字典序输出。
思路：
这道题可以用拓扑排序来做、、拓扑排序是一定的，但是我们的拓扑排序里面是要用到大根堆，而且我们是逆向来存的层数、、、
首先显而易见是拓扑排序.但是考虑到要让前面的数尽量小。我们就不可以采用正向建图了、、
　举个例子:
　1　　　　　　　　　　　　　　　　　我们得到了下面这样一个图、、
　5 4　　　　　　　　　　　　　　　 正向建图得到的点的次序是1 4 5 3 2

　1 4　　　　　　　　　　　　　　　  1到n的质量为1 5 4 3 2　　
　4 2　　　　　　　　　　　　　　　　正确答案为1 5 3 4 2
　5 3　　　　　　　　　　　　
　3 2　　　　　　　　　　　　　　　　为什么？！

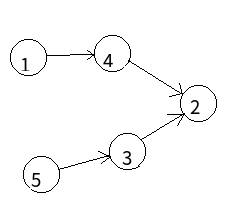　　　　　　　　我们正向建图时，1出去以后的入度为0的点只有4  5我们并没有考虑到5还指向3于是我们an小根堆先选择了4 这样就会造成错误、、、 所以我们这个地方就要反向建图，当然这也就决定了我们要用大根堆、、、、这样我们每次把标号最大的放在后面就可以很好地解决字典序这个问题

注意：我们这个地方输出的是他们的质量、、、、、

代码：

#include<queue>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#define N  41000
using namespace std;
priority_queue<int>q;
int n,m,x,y,s,t,tot,sum,in[N],ans[N],head[N];
int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1; ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0'; ch=getchar();}
    return x*f;
}
struct Edge
{
    int from,to,next;
}edge[N];
void add(int x,int y)
{
    tot++;
    edge[tot].to=y;
    edge[tot].next=head[x];
    head[x]=tot;
}
void begin()
{
    sum=0,tot=0;
    memset(in,0,sizeof(in));
    memset(ans,0,sizeof(ans));
    memset(edge,0,sizeof(edge));
    memset(head,0,sizeof(head));
}
int main()
{
    t=read();
    while(t--)
    {
        begin();
        n=read(),m=read();
        for(int i=1;i<=m;i++)
        {
            x=read(),y=read();
            in[x]++,add(y,x);
        }
        for(int i=1;i<=n;i++)
         if(in[i]==0) q.push(i);
        tot=n;
        while(!q.empty())
        {
            x=q.top(),q.pop();ans[x]=tot;
            tot--;sum++;
            for(int i=head[x];i;i=edge[i].next)
            {
                int t=edge[i].to;
                in[t]--;
                if(in[t]==0) q.push(t);
            }
        }
        if(sum!=n) printf("-1\n");
        else 
        {
            for(int i=1;i<n;i++)
             printf("%d ",ans[i]);
            printf("%d\n",ans[n]);
        }
    }
    return 0;
}

 

转载于:https://www.cnblogs.com/z360/p/7420218.html