讲座嘉宾:Steve
讲座链接:ACM大神精讲最新北美Google Facebook面试题
讲座总结:6Kunnnnn
题目1 Five in a Row
题目介绍

其实这道题目就是五子棋的规则,条件就是横竖或者对角线满足5个同样棋子,很好理解。
题目分析
首先,我们能想到的就是暴力枚举法,也就是枚举棋盘上各个棋子,判断是否能够满足条件。每个棋子有8个方向,但是我们需要除去冗余的枚举,只考虑4个方向就好了。如下图:
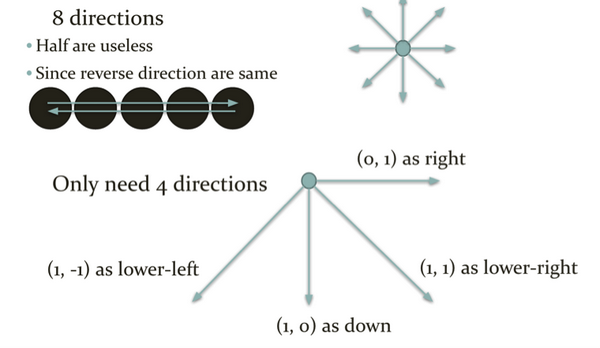
那么,我们需要一个数组处理方向,如下图,其中d(k)就是用来表达方向的数组,注:下图中 d(2) = (1, -1) 应该为 d(3) - (1, -1) 即lower-left的方向
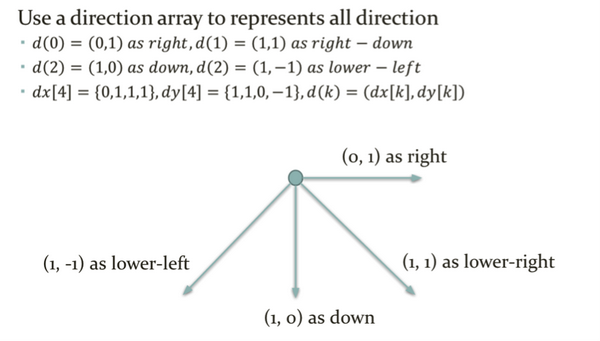
那么给定点(x, y),和方向(dx[k], dy[k]),在这个方向上的第N个棋子就是 (x + dx[k] * N, y + dy[k] * N),如下图:
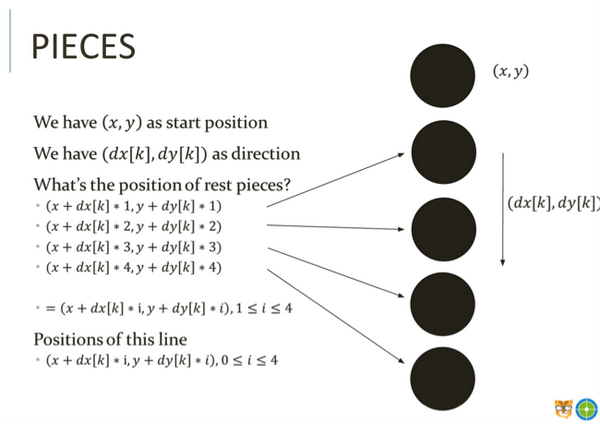
现在有了知道一个棋子某个方向上某个点的位置的方法,我们就可以判断对于任意棋子的4个方向上,是否有满足条件的情况。对于最后的输出结果,我们要判断对于黑白两种棋子,是否分别存在满足条件的情况。如下图:

所以总结起来,我们需要枚举每个棋子的四个方向上,每一个可能位置,并检查是否成立,这个算法的复杂度是N方,因为需要对每一个棋子都进行判断。如下图:

代码实现
如下图,valid(x, y) 判断棋子位置是否合法,也就是不能超过棋盘的范围,比如这道题目中棋盘长和宽都是15。

算法优化

如上图,暴力解法虽然直白,但是复杂度不尽人意。比如如果不是五子棋,而是M子棋,时间复杂度就会变大。如何优化呢?首先要了解暴力解法的弊端是什么:简单来说,就是存在有些棋子被重复判断的情况。而有一种更好方法是,从各个方向上判断是否存在某一颜色的棋子成立M行的情况。如下图,我们假定还是五子棋的情况,即M=5,给定某个点的坐标(x, y),方法Black(x, y)用来判断从(x, y)这个点对于横行向右的方向上,连续黑色棋子的个数,具体实现如下图,是通过递归来完成,isBlack(x, y)用来判断(x, y) 坐标是否为黑子,是则返回1否则0。同理White和isWhite方法。

该算法的实现如下图:Step1,枚举每一个方向,而不是棋子本身;Step2,逆向枚举每个方向上的棋子,即x和y都是从N到1;Step3,用递归的方法来计算某个方向上的不同颜色的棋子个数;Step4,只有这步和之前的暴力解法一样,判断最终的结果。算法最终复杂度为N方,不涉及M的参与。
题目2 Building Heap
题目介绍

给出一个最小堆的中序遍历,来生成这个最小堆,并且输出它的前序遍历的结果。输入就是,一个Int数组来存储中序遍历最小堆的结果,比如7 6 8 1 3 11,输出就是打印出这个最小堆的前序遍历,就是1 6 7 8 3 11。
题目分析
先来回顾一下Heap的性质。Heap在结构上是一个二叉树,所谓的最小堆Min-Heap,就是指从root节点开始,parent节点的值永远小于child节点。既然Heap是一种树,那么当然存在各种顺序的遍历traversal。总的来说,无论是In-Order还是Pre/Post-Order,这里的Order对应的是root/parent节点的Order,比如中序遍历是指先left-subtree,然后root,最后right-subtree。
既然root节点的值肯定比其他节点要小,也就是这个数组中的最小值1。之后,根据中序遍历的规律,root的左子树在root前边先被遍历,右子树则刚好相反。那我们知道了root节点为1后,就可以判断,在1前边就是这个堆的左子树,后边的就是右子树。如下图:
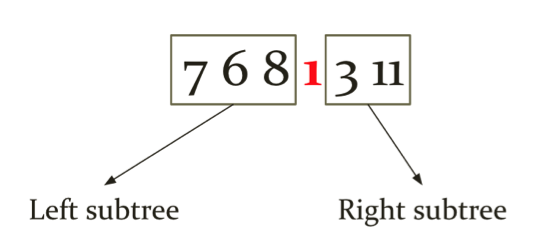
这道题目是一道递归题,考查的是分治思想Divide & Conquer,就是把之前的大问题,转化成若干性质相同的小问题,然后找到小问题的答案,最后将答案合并到一起就是大问题的答案。对于此题,最初的大问题就是最开始的input 7 6 8 1 3 11,而我们上边所讲的,先找到root,再找到左右子树,然后对左右子树递归,这里“左右子树分别递归”就是被分解成的小问题。所以对于此题,我们可以分解为三个步骤,如下图: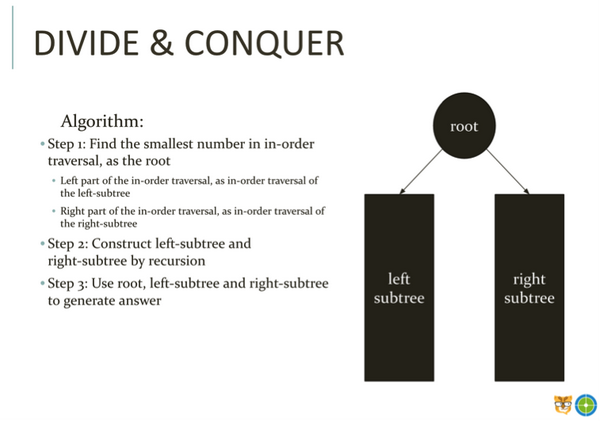
那么这种算法的时间复杂度是多少?首先,对于分治思想,一个很重要的概念就是层Level,可以理解为是将大问题分解成小问题所需要的次数,等价于树的高度Height,而对于树Tree来说,高度是一个很重要的性质。所以对于此算法,我们需要考虑将大问题分解成小问题的层数,也要考虑每一层的计算次数。如下图:
假定输入里有N个元素的话,对于每一层来说,都需要找到最小node,这需要O(N)的复杂度。对于层数,平均情况是logN层,就是这个树是左右对称的。而最坏情况是N层,就是这个Tree其实是一个chain,比如下图: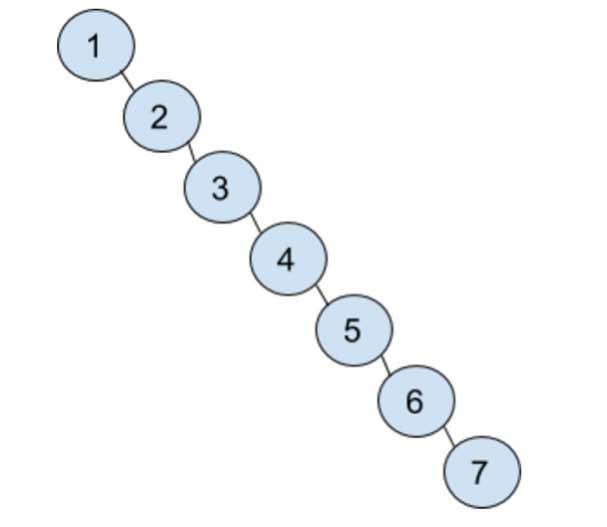
代码实现

算法优化
其实对于这个题目,我们可以避免创建Min-Heap,而是直接把结果打印出来,如下图:
而如何避免最坏情况的发生?可以用RMQ,Range Minimum Query这个数据结构。感兴趣的同学可以自学一下。
题目3 Guess Number with Lower or Higher Hints

这是一道DP的题目,很有难度,欢迎各位去观看原视频内容!
设立于硅谷,专注于编程、数据分析、UIUX设计的在线学习平台:BitTiger。




 本文解析了两道经典算法题目:五子棋判定胜利条件和根据中序遍历构建最小堆并输出前序遍历结果。针对每道题目,文章详细介绍了题目背景、分析思路、代码实现及优化方案。
本文解析了两道经典算法题目:五子棋判定胜利条件和根据中序遍历构建最小堆并输出前序遍历结果。针对每道题目,文章详细介绍了题目背景、分析思路、代码实现及优化方案。


















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








