bzoj4916 神犇和蒟蒻

最新推荐文章于 2019-02-27 13:12:00 发布

weixin_33787529

最新推荐文章于 2019-02-27 13:12:00 发布

阅读量50

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/yzxverygood/p/10089040.html

本文深入探讨了数论算法中的一种高效求解欧拉函数的方法，通过预处理和递归调用，实现对大规模数据的快速处理。代码示例清晰展示了算法的实现细节，包括初始化、递归函数和主函数部分，为读者提供了完整的解决方案。

传送门

分析

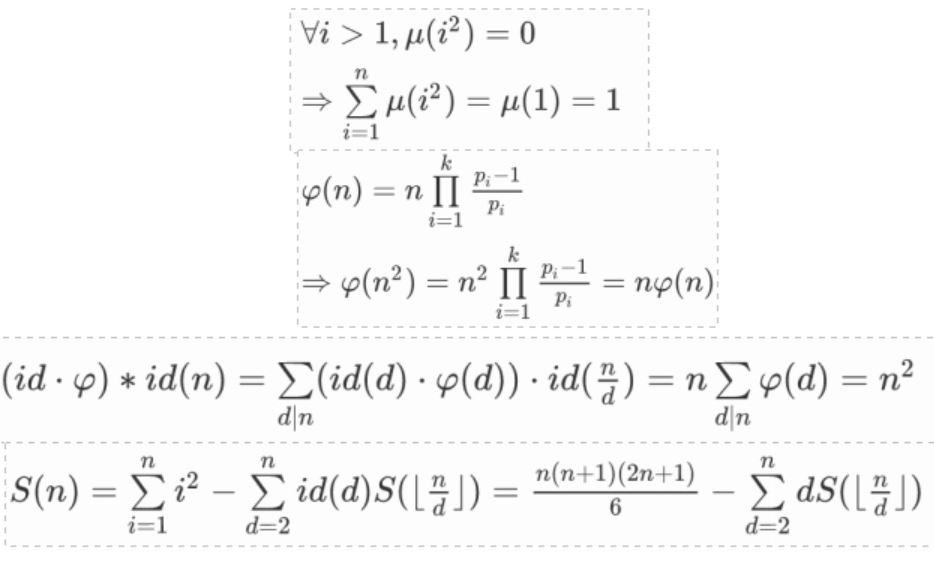
代码

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<algorithm>
#include<cctype>
#include<cmath>
#include<cstdlib>
#include<queue>
#include<ctime>
#include<vector>
#include<set>
#include<map>
#include<stack>
using namespace std;
const int mod = 1e9+7;
const int N = 5e6;
int p[N+10],phi[N+10];
bool is[N+10];
map<int,int>Ans;
inline void init(){
    int i,j,cnt=0;
    phi[1]=1;
    for(i=2;i<=N;i++){
      if(!is[i])p[++cnt]=i,phi[i]=i-1;
      for(j=1;j<=cnt,p[j]*i<=N;j++){
          is[i*p[j]]=1;
          if(i%p[j]==0){
            phi[p[j]*i]=(long long)phi[i]*p[j]%mod;
            break;
          }
          phi[p[j]*i]=(long long)phi[i]*(p[j]-1)%mod;
      }
    }
    for(i=2;i<=N;i++)phi[i]=(phi[i-1]+(long long)phi[i]*i%mod)%mod;
}
inline int go(int x){
    if(x<=N)return phi[x];
    if(Ans[x])return Ans[x];
    long long mm=(long long)mod*6;
    int res=(long long)x*(x+1)%mm*(2*x+1)%mm/6%mod,le=2,ri;
    for(;le<=x;le=ri+1){
      ri=x/(x/le);
      int kk=(long long)(ri-le+1)*(le+ri)/2%mod;
      res=(res-(long long)kk*go(x/le)%mod+mod)%mod;
    }
    return Ans[x]=res;
}
int main(){
    int n;
    scanf("%d",&n);
    init();
    puts("1");
    cout<<go(n);
    return 0;
}