第三周作业

一.基础作业

本周请大家完成上周挑战作业的第一部分：给定一个整数数组(包含正负数)，找到一个具有最大和的子数组，返回其最大的子数组的和。

例如：[1, -2, 3, 10, -4, 7, 2, -5]的最大子数组为[3, 10, -4, 7, 2]
输入：

请建立以自己英文名字命名的txt文件，并输入数组元素数值，元素值之间用逗号分隔。

输出

在不删除原有文件内容的情况下，将最大子数组以及子数组的和写入文件。

1.实验代码

#include<stdio.h>
#include<stdlib.h>
int main ()
{

  FILE *fp;   //定义文件指针 
  int n,i,j,head,tail;  
 int nums[1000];
   int sum = 0;   //初始和为0
   int max = 0;//最大值最初必为数组第一个元素
  if((fp=fopen("F:\\第三周基础作业f505-Yangling.txt","w+"))==NULL)  //建立新文本文件进行读或写 
  {
        printf("File open  error!\n");
        exit(0);
  }
   scanf("%d\n",&n);     //输入一维数组中元素的个数 
   fprintf(fp,"%d\n",n);
    
   for(i=0;i<n;i++)
   {
        scanf("%d",&nums[i]);
        fprintf(fp,"%d ",nums[i]);
    }    
        
    for(i=0;i<n;i++)
    {
        sum = sum + nums[i];  //遍历一个元素，累加一次 
    
        if(sum < nums[i])//如果加上当前元素之后的和比当前元素还小，则舍弃之前的元素，从当前元素开始累加
        {
            sum = nums[i];
        }
        //如果加上当前元素之后的和比当前元素大
        //说明可以继续累加
        //如果当前和比最大值大，则更新最大值为当前和
        //否则，不做更新
        if(sum > max)
        {
            max = sum;
        }
        
    } 
    for(i=0;i<n;i++)
    {
        sum=0;
        for(j=i;j<n;j++)
        {
            sum=sum+nums[j];
            if(sum==max)    //这里是将最大数组的首尾记录下来 
            {              
               head=i;
               tail=j;
               break;
            }

        }
    }
    fprintf(fp,"\n最大子数组是");
    for(i=head;i<=tail;i++)   //把前面记录的首尾作为范围来打印子数组 
      {
      fprintf(fp,"%d,",nums[i]);
    
}
  fprintf (fp,"\n%d",max);   //打印最大值 

  
  if(fclose(fp))
  {
        printf("Can not close the file!\n");
        exit(0);
  }
   return 0;
}

2.设计思路：

流程图：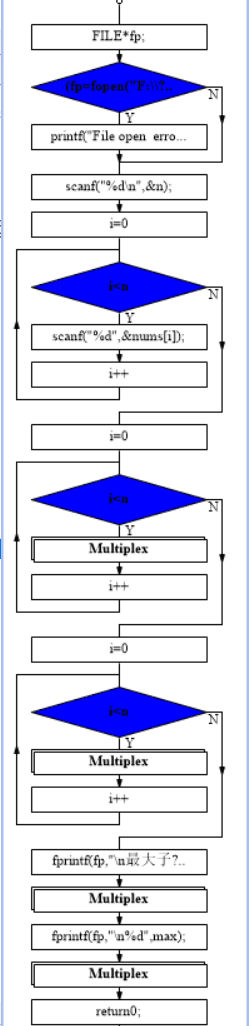

思路：
遍历一个元素，累加一次 ，如果加上当前元素之后的和比当前元素还小，则舍弃之前的元素，从当前元素开始累加
如果加上当前元素之后的和比当前元素大，说明可以继续累加，如果当前和比最大值大，则更新最大值为当前和
否则，不做更新 然后记录当前数的首尾作为范围来打印子数组 最后输出最大子数组和最大值

3.本题遇到的问题及解决办法：

错误截图：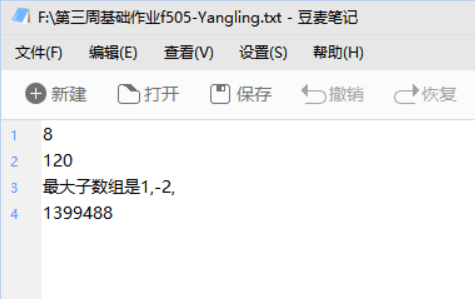

开始不知道怎么弄错了，后来发现输入的时候忘了加括号

不会用二维数组在垂直水平方向上来相连 并且要考虑最佳解法
这次作业比上次多了一个打印最大子数组的要求

4.运行截图：

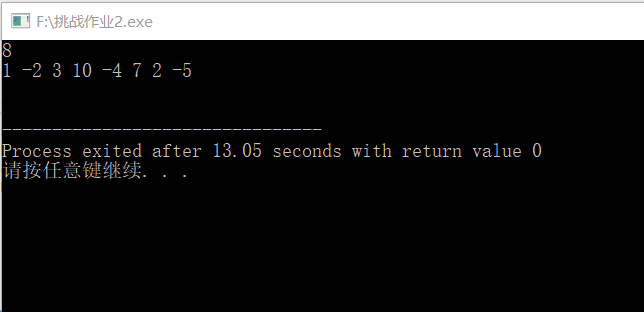
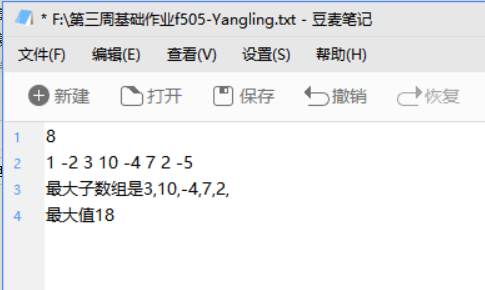
二.预习作业

7-1 判断上三角矩阵 （15 分)

上三角矩阵指主对角线以下的元素都为0的矩阵；主对角线为从矩阵的左上角至右下角的连线。

本题要求编写程序，判断一个给定的方阵是否上三角矩阵。

输入格式：
输入第一行给出一个正整数T，为待测矩阵的个数。接下来给出T个矩阵的信息：每个矩阵信息的第一行给出一个不超过10的正整数n。随后n行，每行给出n个整数，其间以空格分隔。

输出格式：
每个矩阵的判断结果占一行。如果输入的矩阵是上三角矩阵，输出“YES”，否则输出“NO”。

输入样例：

2
3
1 2 3
0 4 5
0 0 6
2
1 0
-8 2

输出样例：

YES
NO

预习可以参看翁恺老师的MOOC视频:(https://www.icourse163.org/course/ZJU-9001) ，第八周 数组—》8.2 数组运算

1.实验代码：

#include <stdio.h>  
int main() 
{  
  int T,n,i,j,k;
    int num[10][10];  //因为n最大为10，所以定义10*10的二维数组
    scanf("%d",&T);  //输入矩阵个数
    int count=0;
    int record[100]={0};  //记录判断记录 
    
    for(k=0; k<T; k++)  //将n行n列数字读入数组 
    {
        scanf("%d",&n);
        for(i=0; i<n; i++){
            for(j=0; j<n; j++){
                scanf("%d",&num[i][j]); 
            }       
        }
        for(i=0; i<n; i++)   //判断矩阵 
        {
            for(j=0; j<n; j++){
                if(i>j && num[i][j] != 0)
                {
                    count++;
                }
            }       
        }
        if(count==0 )
        {
            record[k] = 1;  //代表符合条件
        }else{
            record[k] = 0;  //代表不符合条件
        }
        count=0;        
    }
    
    for(k=0; k<T; k++)  //打印结果
    {
        if(record[k]==1)
        {
            printf("YES\n");
        }else{
            printf("NO\n");
        } 
    }
    
    return 0;  
}

2.设计思路：

流程图：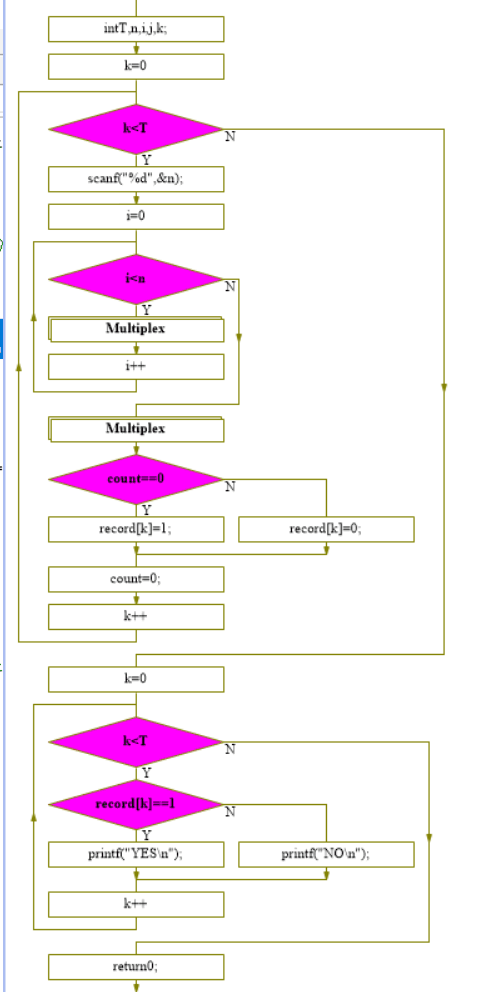

思路：
因为n最大为10，所以定义10*10的二维数组，然后再输入矩阵个数
在用一个数组记录判断记录 接着将n行n列数字读入数组 ， 然后判断矩阵是否为上三角矩阵，
最后再判断是否符合条件

3.本题遇到的问题及解决办法：

首先要了解什么是上三角矩阵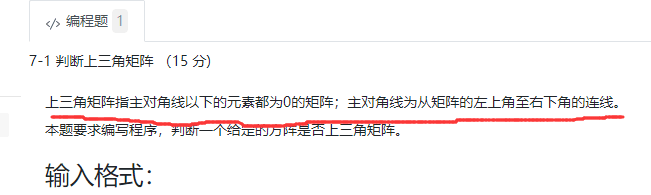

然后要注意一下判断左下角的数要为0
我写这个题目的时候没有遇到什么问题

4.实验结果截图：

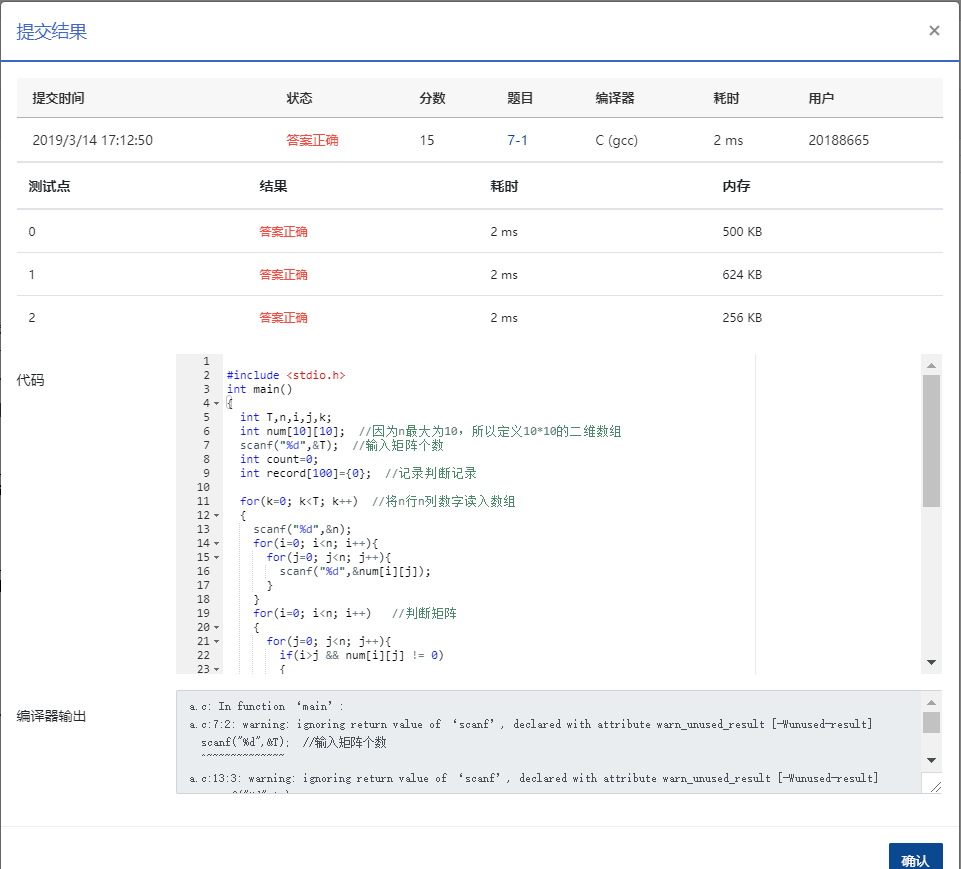
二、学习进度条

周/日期	这周所花的时间	代码行	学到的知识点简介	目前比较迷惑的题目
3/4-3/9	6小时	89	新建文件进行读写	二位数组子数组的最大值的求和
3/10-3/15	8小时	156	二维数组的运用	二位数组子数组的最大值的求和

三、学习感悟

我在这周学了怎么去新建文件 在文件中打印结果，还学了二维数组的使用，但是上次老师的挑战题目我还是不会做

转载于:https://www.cnblogs.com/lyx1314/p/10538531.html