幂集合[集合论]

最新推荐文章于 2022-09-12 14:17:28 发布

weixin_33762130

最新推荐文章于 2022-09-12 14:17:28 发布

阅读量347

点赞数

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/tinaluo/p/5260295.html

本文介绍了一种使用二进制模拟的方法来生成给定集合的所有子集（幂集）。通过一个具体的示例和完整的C++代码实现，展示了如何利用二进制数的变化来枚举所有可能的子集。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

补充：（改进：一种递归方法）http://www.cnblogs.com/tinaluo/p/5294341.html
已知集合S，S的幂集合是指集合S所有子集的集合，用P(S)来表示，例如：

P({0,1,2})={$,{0},{1},{2},{0,1},{0,2},{1,2},{0,1,2}};

这让我想起二进制模拟，假如现在用算法模拟打印幂集合（空集除外），该怎么办呢？
二进制模拟起到很好的作用，首先来看一下，二进制模拟是什么，如图：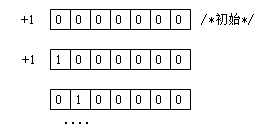
数组初始为0，循环在首位+1，按照二进制格式进位，最终会得到下面的可能：

1　　0　　0　　0　　0
0　　1　　0　　0　　0
1　　1　　0　　0　　0...
假如有3个元素，组合则有7种形式，加上空集，即为幂集合的所有可能性！

/*-------完整代码@映雪-------*/

#include <iostream>
using namespace std;        
int main()
{
    int carry=1;
    int a[3]={0};/*状态数组*/
    int b[3]={0,1,2};/*集合数组*/
    int n=7;
    while(n>0)
    {        
        for(int i=0;i<3;i++)/*每次得到一种状态*/
        {
            a[i]+=carry;
            carry=a[i]/2;
            a[i]=a[i]%2;
            if(carry==0)
            break;
        }
        for(int j=0;j<3;j++)/*遍历数组状态，打印幂集*/
        {
            if(a[j]==1)
            cout<<b[j]<<" ";
        }
        cout<<endl;
        --n;
        carry=1;/*复位*/
    }
    return 0;
}