1、概念

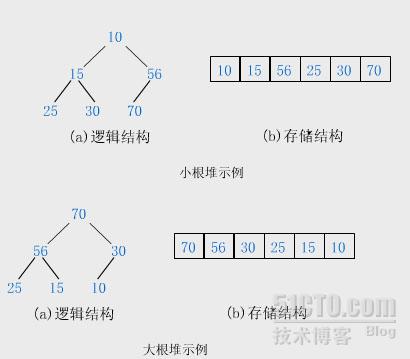
堆：堆是具有下列性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大根堆；或者每个结点的值都小于或等于其左右孩子结点的值称为小根堆。

100649621.jpg

堆排序(Heap Sort)：将待排序的序列构造成一个大根堆。此时，整个序列的最大值就是堆顶的根结点。将它移走(其实就是将其与堆数组的末尾元素交换，此时末尾元素就是最大值)，然后将剩余的n-1个序列重新构造成一个堆，这样就会得到n个元素中的次大值。如此反复执行，便能得到一个有序的序列了。(构造成小根堆也是一样的)

2、code

/*对顺序表L进行堆排序*/
void HeapSort(SqList *L)
{
    int i;
    for(i=L->length/2;i>0;i--)    /*把L中的r构造成一个大根堆，i从0到length/2都是有孩子的结点*/
        HeapAdjust(L,i,L->length);
    for(i=L->length;i>1;i--)
    {
        swap(L,1,i);    /*将堆顶记录和当前未经排序子序列的最后一个记录交换*/
        HeapAdjust(L,1,i-1);    /*将L->r[1…i-1]重新调整为大根堆*/
    }
}

/*已知L->r[s…m]中记录的关键字除L->r[s]之外均满足堆的定义*/
/*本函数调整L->r[s]关键字，使L->r[s…m]成为一个大根堆*/
void HeapAdjust(SqList *L,int s,int m)
{
    int temp,j;
    temp=L->r[s];
    for(j=2*s;j<=m;j*=2)    /*沿关键字较大的孩子结点向下筛选*/
    {
        if(j<m && L->r[j]<L->r[j+1])
            ++j;    /*j为关键字中较大的记录下标*/
        if(temp>=L->r[j])
            break;
        L->r[s]=L->r[j];
        s=j;
    }
    L->r[s]=temp;    /*插入*/
}