POJ 2546 Circular Area 求两圆的重合面积

最新推荐文章于 2018-03-30 17:59:07 发布

转载最新推荐文章于 2018-03-30 17:59:07 发布 · 136 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/evan-oi/archive/2012/03/14/2395989.html

本文介绍了如何使用余弦定理和反余弦函数求解POJ 2546题目中不规则图形的面积问题。通过将问题转化为计算两个楔形区域的面积，利用扇形和三角形面积之差得出解决方案。

题目链接：http://poj.org/problem?id=2546

题目大意：RT。

分析：如图，ACBD就是我们要求的面积，要想直接求显然是不可行的，我们可以把它拆成ACB和ADB两个楔形(是叫这个吧？)，如果首先求ACB的话，只要求出扇形ACB和三角形OAB的面积相减就可以，而想求它们两个的面积就得求出角AOB的度数。怎么求呢，我们可以先用余弦定理求出角AOB的cos值，然后一个NB的东西就出场了(至少我这么想)，cmath～，里面提供了反余弦函数，那我们就可以通过cos值直接得到角度。之后就随便搞一下就可以了。

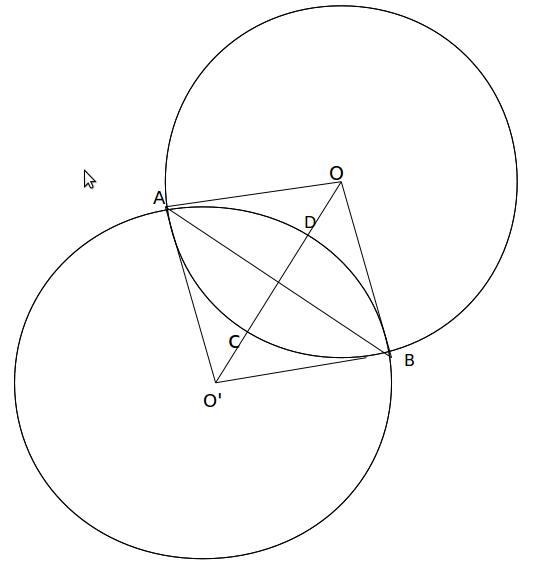
至此问题圆满解决。以后碰到相应的题目还可以当模板用。

附代码：

View Code

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<cmath>
using namespace std;
#define pi 3.141592653
struct point
{
double x,y,r;
    }p[3];

double dis(point a,point b)
{
return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
    }

double calc(point a,point b)
{
double d=dis(a,b);
if (d>=a.r+b.r) return 0;
double r=a.r>b.r?b.r:a.r;
if (d<=fabs(a.r-b.r)) return pi*r*r;
double t1=acos((a.r*a.r+d*d-b.r*b.r)/2.0/a.r/d);
double t2=acos((b.r*b.r+d*d-a.r*a.r)/2.0/b.r/d);
double t=0;
    t-=d*a.r*sin(t1);
    t+=t1*a.r*a.r+t2*b.r*b.r;
return t;
    }

int main()
{
    freopen("in","r",stdin);
    freopen("out","w",stdout);
while(scanf("%lf%lf%lf%lf%lf%lf",&p[1].x,&p[1].y,&p[1].r,&p[2].x,&p[2].y,&p[2].r)!=EOF)  
    {  
double ans=calc(p[1],p[2]);  
        printf("%.3lf\n",ans); 
    }  
return 0;
    }

转载于:https://www.cnblogs.com/evan-oi/archive/2012/03/14/2395989.html