二叉树的镜像

最新推荐文章于 2025-09-10 17:59:49 发布

转载最新推荐文章于 2025-09-10 17:59:49 发布 · 102 阅读

0 ·

CC 4.0 BY-SA版权

原文链接：https://my.oschina.net/u/2260265/blog/344719

文章标签：

#python #数据结构与算法 #测试

本文介绍了一种通过递归方式实现二叉树镜像的方法。通过对二叉树的前序遍历，在遍历过程中交换节点的左右子节点，从而得到原始二叉树的镜像。文中还提供了详细的代码实现及测试案例。

2019独角兽企业重金招聘Python工程师标准>>>

题目：完成一个函数，输入一棵二叉树，该函数输出它的镜像。

为了能够形成直观的印象，可以使用图例进行分析：

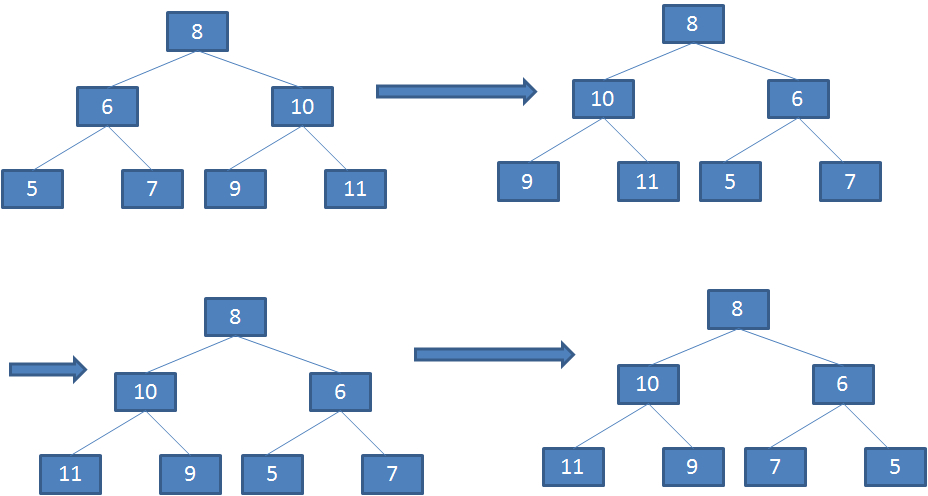
分析第一棵与最后一棵树的特点，能够总结出求镜像的步骤。这两棵树的根节点相同，但他们的左右两个子节点交换了位置。因此，先在树中交换根节点的两个子节点，如上图第二棵树，交换根节点的两个子节点之后，值为 10,6 的节点的子节点仍然保持不变，因此，还需要交换这两个节点的左右子节点。交换之后分别为上图的第三棵和第四棵树。做完这两次交换之后，已经遍历完所有的非叶子节点。此时变换之后的树刚好就是原始树的镜像。

总结上述过程，得出求一棵树的镜像的过程：先前序遍历这棵树的每个节点，如果遍历到的节点有子节点，就交换它的两个子节点，当交换完所有非叶子结点的左右子节点之后，就得到了树的镜像。

//二叉树的镜像
#include<iostream>
using namespace std;

typedef int ElemType;
typedef struct TNode
{
ElemType value;
TNode *LeftChild;
TNode *RightChild;
}TreeNode, *BinaryTree;

//二叉查找树
TreeNode* InsertBinaryTree(BinaryTree T, ElemType e)
{
if(T == NULL)
{
  T = new TreeNode();
  T->value = e;
  T->LeftChild = NULL;
  T->RightChild = NULL;
}
else if(T->value > e)
  T->LeftChild = InsertBinaryTree(T->LeftChild, e);
else if (T->value < e)
  T->RightChild = InsertBinaryTree(T->RightChild, e);
return T;
}

TreeNode* BinaryTreeNode(ElemType e)
{
TreeNode *T = new TNode();
T->value = e;
T->LeftChild = NULL;
T->RightChild = NULL;
return T;
}

void ConnectTreeNode(TreeNode *pParent, TreeNode *pLeft, TreeNode *pRight)
{
if(pParent == NULL)
return;
pParent->LeftChild = pLeft;
pParent->RightChild = pRight;
}

void MirrorRecursively(BinaryTree T)
{
if(T == NULL)
  return;
if(T->LeftChild == NULL && T->RightChild == NULL)
  return;
TreeNode *pNode = T->LeftChild;   //如果T 的左右孩子非空，则交换左右孩子
T->LeftChild = T->RightChild;
T->RightChild = pNode;
if(T->LeftChild)     //T 的左子树非空，递归交换左子树的左右孩子
  MirrorRecursively(T->LeftChild);
if(T->RightChild)
  MirrorRecursively(T->RightChild);
}

void PreOrderTree(BinaryTree T)
{
if(T == NULL)
  return;
cout << T->value << " ";
if(T->LeftChild != NULL)
  PreOrderTree(T->LeftChild);
if(T->RightChild != NULL)
  PreOrderTree(T->RightChild);
}

void DestroyTree(BinaryTree T)
{
if(T != NULL)
{
TreeNode *pLeft = T->LeftChild;
TreeNode *pRight = T->RightChild;

delete T;
T = NULL;

DestroyTree(pLeft);
DestroyTree(pRight);
}
}

//测试用例 Test1（）：一棵普通的二叉树；Test2（）：只有一个根节点的二叉树；Test3（）：空树（即只有一个空指针）
void Test1()
{
TreeNode *Node1 = BinaryTreeNode(8);
TreeNode *Node2 = BinaryTreeNode(6);
TreeNode *Node3 = BinaryTreeNode(10);
TreeNode *Node4 = BinaryTreeNode(5);
TreeNode *Node5 = BinaryTreeNode(7);
TreeNode *Node6 = BinaryTreeNode(9);
TreeNode *Node7 = BinaryTreeNode(11);

ConnectTreeNode(Node1, Node2, Node3);
ConnectTreeNode(Node2, Node4, Node5);
ConnectTreeNode(Node3, Node6, Node7);

cout << "树的前序遍历为：";
PreOrderTree(Node1);
cout << endl;

MirrorRecursively(Node1);
cout << "树的镜像的前序遍历为：";
PreOrderTree(Node1);
cout << endl;
}

void Test2()
{
TreeNode *T = BinaryTreeNode(8);

ConnectTreeNode(T, NULL, NULL);

cout << "树的前序遍历为：";
PreOrderTree(T);
cout << endl;

MirrorRecursively(T);
cout << "树的镜像的前序遍历为：";
PreOrderTree(T);
cout << endl;
}

void Test3()
{
TreeNode *T = NULL;
MirrorRecursively(T);
}

void Test4()
{
TreeNode *T = NULL;
int data;
while(cin >> data)
{
T = InsertBinaryTree(T, data);
}

cout << "树的前序遍历为：";
PreOrderTree(T);
cout << endl;

MirrorRecursively(T);
cout << "树的镜像的前序遍历为：";
PreOrderTree(T);
cout << endl;
}

int main()
{
Test1();
Test2();
Test3();
Test4();

system("pause");
return 0;
}

转载于:https://my.oschina.net/u/2260265/blog/344719