1.本人观看了慕课网上的星级评分视频,课程免费,老师讲的特别棒!视频链接:https://www.imooc.com/learn/842
2.在学习完视频后找到了一位大神手敲的代码,在他的Github上下载后,自己手动实现了一遍。源代码稍后贴出原作者的给的链接:http://www.cnblogs.com/fazero/p/8316926.html
3.本人手动模仿实现了一遍代码,学习了好多,再次只贴出最终的可以点亮整颗星与半颗星的javascript代码,如有雷同版权为原作者所有:
<script src="http://libs.baidu.com/jquery/1.11.3/jquery.min.js"></script>
<script type="text/javascript">
var rating = (function() {
//继承
var extend = function(subClass, superClass) {
var F = function() {};
F.prototype = superClass.prototype;
subClass.prototype = new F();
subClass.prototype.construtor = subClass;
}
//点亮
var Light = function(el, options) {
this.$el = $(el);
this.$item = this.$el.find('.rating-item');
this.opts = options;
this.add = 1;
this.selectEvent = 'mouseover';
}
Light.prototype.init = function() {
this.lightOn(this.opts.num);
if(!this.readOnly) {
this.bindEvent();
}
}
Light.prototype.lightOn = function(num) {
var num = parseInt(num);
this.$item.each(function(index) {
if(index < num) {
$(this).css('background-position', '0 -40px');
} else {
$(this).css('background-position', '0 0');
}
});
}
Light.prototype.bindEvent = function(e) {
var self = this,
itemLength = self.$item.length;
self.$el.on(self.selectEvent, '.rating-item', function(e) {
var $this = $(this),
num = 0;
self.select(e, $this);
num = $(this).index() + self.add;
self.lightOn(num);
(typeof self.opts.select === 'function') && self.opts.select.call(this, num, itemLength);
self.$el.trigger('select', [num, itemLength]);
}).on('click', '.rating-item', function() {
self.opts.num = $(this).index() + self.add;
(typeof self.opts.chosen === 'function') && self.opts.chosen.call(this, self.opts.num, itemLength);
self.$el.trigger('chosen', [self.opts.num, itemLength]);
}).on('mouseout', function() {
self.lightOn(self.opts.num);
})
}
Light.prototype.select = function() {
throw new Error('子类必须重写此方法');
}
Light.prototype.unbindEvent = function() {
this.$el.off();
}
//点亮整颗
var LightEntire = function(el, options) {
Light.call(this, el, options)
this.selectEvent = 'mouseover';
}
extend(LightEntire, Light);
LightEntire.prototype.lightOn = function(num) {
Light.prototype.lightOn.call(this, num);
}
LightEntire.prototype.select = function() {
self.add = 1;
}
//点亮半颗
var LightHalf = function(el, options) {
Light.call(this, el, options)
this.selectEvent = 'mousemove';
}
extend(LightHalf, Light);
LightHalf.prototype.lightOn = function(num) {
var count = parseInt(num),
isHalf = count !== num;
Light.prototype.lightOn.call(this, count);
if(isHalf) {
this.$item.eq(count).css('background-position', '0 -80px');
}
}
LightHalf.prototype.select = function(e, $this) {
if(e.pageX - $this.offset().left < $this.width() / 2) {
this.add = 0.5;
} else {
this.add = 1;
}
}
// 默认参数
var defaults = {
mode: 'LightEntire',
num: 0,
readOnly: false,
select: function() {},
chosen: function() {}
}
var mode = {
'LightEntire': LightEntire,
'LightHalf': LightHalf
}
//初始化
var init = function(el, option) {
//option可以是object、string
var $el = $(el),
rating = $el.data('rating'),
options = $.extend({}, defaults, typeof option === 'object' && option);
if(!mode[options.mode]) {
options.mode = 'LightEntire';
}
if(!rating) {
//如果还没有实例化,就实例化
$el.data('rating', (rating = new mode[options.mode](el, options)));
rating.init();
}
if(typeof option === 'string') {
rating[option]();
}
}
$.fn.extend({
rating: function(option) {
return this.each(function() {
init(this, option);
})
}
})
return {
init: init
};
})();
rating.init('#rating', {
mode: 'LightHalf',
num: 2.5,
chosen: function() {
rating.init('#rating', 'unbindEvent');
}
})
$('#rating2').rating({
mode: 'LightHalf',
num: 3.5
})
$('#rating3').rating({
mode: 'LightHalf',
num: 3.5
})
$('#rating').on('select', function(e, num, total) {
console.log(num + '/' + total)
}).on('chosen', function(e, num, total) {
console.log(num + '/' + total);
})
</script>
最后的运行结果:
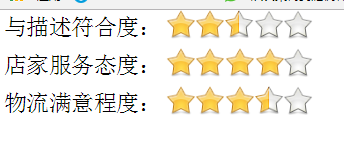







 本文介绍了一个基于jQuery的星级评分组件的实现方法,包括如何通过JavaScript控制星星的点亮状态,支持整颗和半颗星星的显示,并提供了完整的代码示例。
本文介绍了一个基于jQuery的星级评分组件的实现方法,包括如何通过JavaScript控制星星的点亮状态,支持整颗和半颗星星的显示,并提供了完整的代码示例。
















 9687
9687

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








