面试中遇到这样一个算法题,每层拆成父节点的和,最小是1(父节点是1的节点不要再拆了,因为只能拆成0和0,乘积是0,再相加没有意义了),最大是父节点-1。:
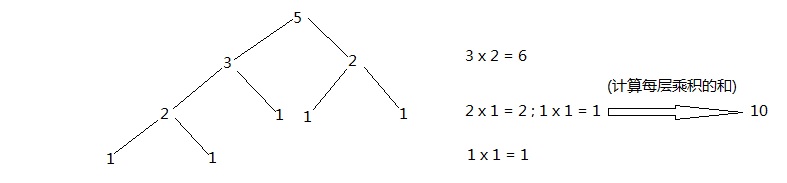
我的解法,使用递归求解:
package com.company; import java.util.Random; /** * 求树中每层乘积的和的算法 * * @Auther: Liu Zhong Jun * @Date: Created In 2017/12/24 17:58 * @Modified By: */ public class TreeSum { public static void main(String[] args) { System.out.println(sum(100)); } public static long sum(int n) { if (n == 1) { return 0L; } int left = random(n); int right = n - left; return left * right + sum(left) + sum(right); } private static int random(int n) { if (n == 1) return 0; if (n == 2) return 1; int rand = new Random().nextInt(n); if (rand == 0) return 1; return rand; } }
当然,以上无疑是正确的,但是算法复杂度是O(n2),是面试官推导的。惭愧。
其实,这里有个规律,就是子节点无论怎么拆,结果(和)都是一样的。(不信你试试)
要想提高算法的效率,我们可以变通一下,看下面的树:
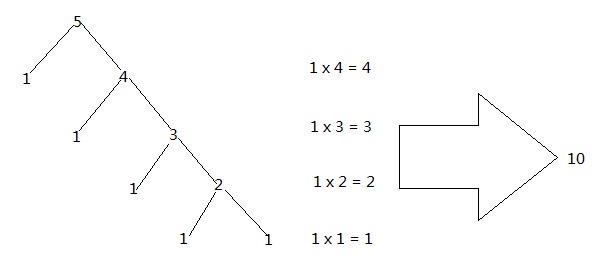
大家发现规律了吧,只要计算右边顶点的和就可以了,这样将递归和里面的乘法转换等差数列了。既简单,效率又高。
等差数列的计算公式是:
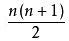
时间复杂度是:longn/2




 本文介绍了一种关于树形结构的算法题,通过递归方式求解每层节点乘积之和的问题,并给出了一种更高效的算法实现思路,即将递归转化为等差数列计算,大大提高了算法效率。
本文介绍了一种关于树形结构的算法题,通过递归方式求解每层节点乘积之和的问题,并给出了一种更高效的算法实现思路,即将递归转化为等差数列计算,大大提高了算法效率。
















 1009
1009

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








