数据结构之六度空间

实验题目:

“六度空间”理论又称作“六度分隔（Six Degrees of Separation）”理论。这个理论可以通俗地阐述为：“你和任何一个陌生人之间所间隔的人不会超过六个，也就是说，最多通过五个人你就能够认识任何一个陌生人。”

也就是在无向图中，以节点作为人，两个节点之间的路径小于等于6。

实验要求
求出与一个节点满足上述要求的其他节点的数目，初始值为1

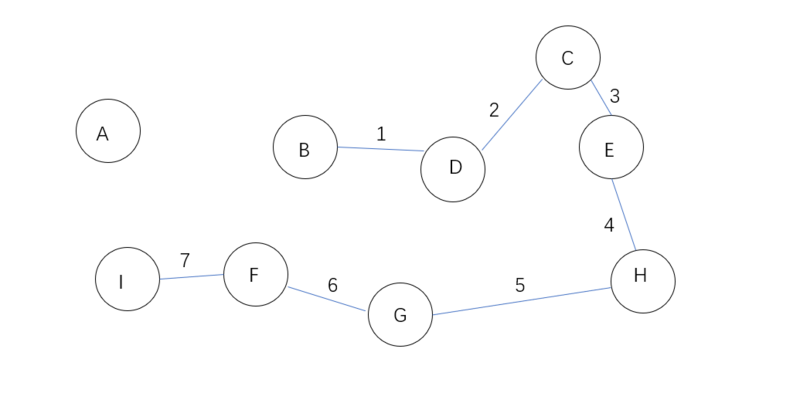
如图 以A， B为例
A: 没有与A满足上述条件的点.因此。A节点的值为0
B: D C E H G F都满足条件 因此B节点的值就是7

实验思路：
即无向图的广度优先遍历

1.图的存储

书上讲过无向图的存储最好是邻接多重链表，但是看起来比较麻烦，我就偷懒用了邻接表来存储

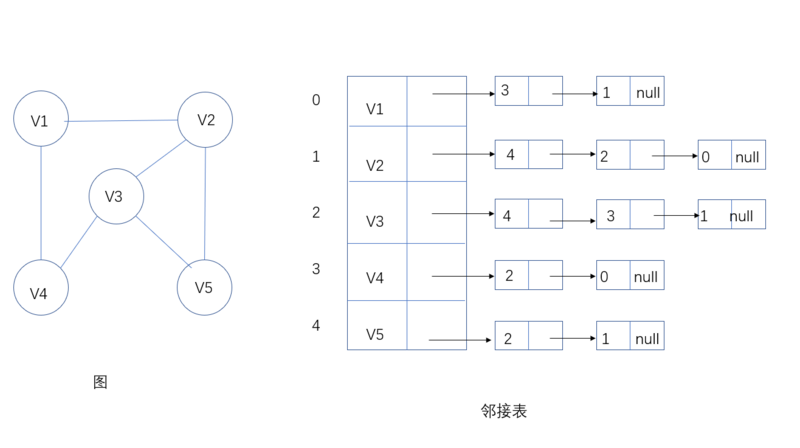
创建方式，定义表头节点和表节点

    typedef struct EdgeNode
    {
        int adjvex;
        struct EdgeNode * next;
    } EdgeNode;
    
    //顶点表节点结构，tag用来判定是否被遍历过，一个firstedge是用来指向边表的第一个节点
    typedef struc