为何比较排序突破不了O(nlgn)

为什么80%的码农都做不了架构师？>>>   

题记：

         根据百度的说法，排序是计算机内经常进行的一种操作，其目的是将一组“无序”的记录序列调整为“有序”的记录序列。【1】排序可以按照进行过程中是否比较输入的元素又分为比较排序(Comparision Sorts)和非比较排序(Operation Sorts, Use operations other than comparisions to determine the sorted order)。【2】再讲得白一点，比较排序的典型代表就是大家常见的时间复杂度不小于O(nlgn)的排序，比如冒泡、插入、选择、快排、归并、堆排序以及上述提到排序的优化版等；而非比较排序比如桶排序、基数排序等。那么，为什么比较排序的时间复杂度会大于O(nlgn)，然而非比较排序的时间复杂度就有望突破这个极限呢？

一、谈谈斯特林公式

        斯特林公式为我们提供了估计n全排列的值的一种方式，对于经常进行算法分析（分析各种排序结果可能性的人）比较有帮助。关于此公式的详解，限于篇幅这里就不展开了。感兴趣的童鞋请自行阅读《算法导论》第三版第53页至第58页的相关内容，也可以到百度搜索一下简单了解。需要说明的是，这里我们重点介绍斯特林公式的以下形式：

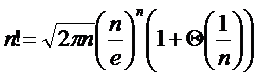
这个公式把n的全排列写成了一个根式、一个指数式和一个有理式。由于Theta(1/n)是次要项，我们可以看到在之后的计算中它实质上是可以忽略的。那么，这个公式跟这个极限之间到底存在着什么样的关系呢？

 

二、再说排序

        排序是什么？站在程序猿的角度可能就仅限于前文所说把混乱的数据按照一定规则变得有序。然而站在数学分析的角度就不同了。

这张来自《算法导论》第三版192页的插图很好地说出了排列数据的数学本质。就是在n个元素的全排列中找到唯一的一个把n个元素按照一定顺序排列的数组的过程。我们可以看到这个过程是用判定树进行记录的。以3个元素的排序为例。首先要把第一个元素与第二个元素比较，结果会有大于和不大于，分别从两个分支进入判定树下一深度的节点。如果上一步中第一个元素不大于第二个元素，则将第2、3个元素依次比较；否则第1、3个元素进行比较，第二深度结束以后按照相应的分支得出比较结果或继续比较。所有的比较结果记录在叶子节点中，以排列完毕的数组的形式呈现。

        通过分析此过程，我们就可以知道事实上从根节点到叶子节点的深度就代表了对于某个特定输入通过比较排序法进行比较的次数。叶子节点的即n的各种全排列的可能性，数目为n!。

 

三、“比较排序”的症结在哪

        有了前面两部分知识的积累，我们就可以分析导致比较排序突破不了O(nlgn)的极限在哪里了。我们知道对于任意一棵二叉树，假设叶子节点数量为k，二叉树的深度为h，那么一定有以下公式：

其中等号成立时此二叉树称为完全满二叉树(Complete and Full Binary Tree)。【3】具体到整个排序的过程，第二部分已经很清楚地说明了这里的k值为n!。因此对于比较排序，我们可以得到如下公式：

两边取对数（以2为底还是以自然数底数为底在这里是不重要的，造成的差异为常数级别，可忽略），可得：

又根据第一部分提到的斯特林公式，我们可以对于lg(n!)作如下缩放处理：

经过几步简单的代数运算之后，我们就不难得出以下结论：

这就说明了比较排序的最坏时间复杂度为O(nlgn)。因此，比较排序症结在哪里就豁然开朗了。对相邻元素的比较确实节省了空间，比较的过程却悄悄地构造了一棵庞大的判定树，虽然重点只是树的高度，然而痛苦却定格在了此处。算法的世界往往如此，大部分情况下想要节省时间就休想节省空间，反之亦然，真可谓“鱼和熊掌不可兼得”。

 

参考资料：

1.百度百科

2.《算法导论》第三版

3. 《数据结构与算法分析（C++版）》第三版

转载于:https://my.oschina.net/Samyan/blog/725665