某次考试考到
超级卡特兰数(又称大施罗德数)
意义:F[n]:从(0,0)开始,只能往上往右或者往右上,不能跨过y=x,到达(n,n)的路径方案数
递推式的证明:
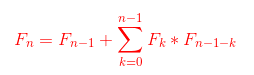
类比卡特兰数,后面的是枚举第一次碰到y=x在哪里
还要加上一个F(n-1)的原因是,并没有统计第一次斜着走到(1,1)的情况,之前统计的都是第一次横着走的。
 本文探讨了超级卡特兰数(大施罗德数)的概念及其递推式的证明过程。超级卡特兰数F[n]表示从起点(0,0)到终点(n,n),仅能向上、向右或向右上方移动且不跨越y=x线的路径方案数量。文章通过类比卡特兰数,详细解析了递推式中每部分的意义。
本文探讨了超级卡特兰数(大施罗德数)的概念及其递推式的证明过程。超级卡特兰数F[n]表示从起点(0,0)到终点(n,n),仅能向上、向右或向右上方移动且不跨越y=x线的路径方案数量。文章通过类比卡特兰数,详细解析了递推式中每部分的意义。
某次考试考到
意义:F[n]:从(0,0)开始,只能往上往右或者往右上,不能跨过y=x,到达(n,n)的路径方案数
递推式的证明:
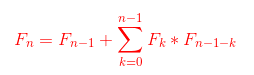
类比卡特兰数,后面的是枚举第一次碰到y=x在哪里
还要加上一个F(n-1)的原因是,并没有统计第一次斜着走到(1,1)的情况,之前统计的都是第一次横着走的。
转载于:https://www.cnblogs.com/Miracevin/p/10260908.html
 615
615
 1109
1109
 1163
1163

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


