统计章节的几个难点

一、以前的各自的算法：

0、利用频率分布直方图计算众数、中位数、平均数、方差当将一组数据制作成频率分布直方图时，数据信息会有所损失，故相关数据的求解会和前面所用的方法有点不太一样了。

二、频率分布直方图中的算法

1、方差：以计算出的平均数为依托，代入公式求解。

2、众数：直方图中最高矩形的中点横坐标

3、中位数：中位数就是频率分布直方图面积的一半所对应的值，即面积等分线所对应的横坐标。

4、平均数：每个矩形的分组的中点值乘以每个对应矩形的面积再求和。

5、给定频数分布表求平均数：每个矩形的分组的中点值乘以频数再求和，最后除以样本容量。

6、给定频率分布表求平均数平均数：每个矩形的分组的中点值乘以每个对应矩形的频率再求和。

三、典例剖析

例1【2017高考真题卷Ⅱ文科19题改编】【题文】如右图所示，求该频率分布直方图的众数、中位数、平均数、方差。

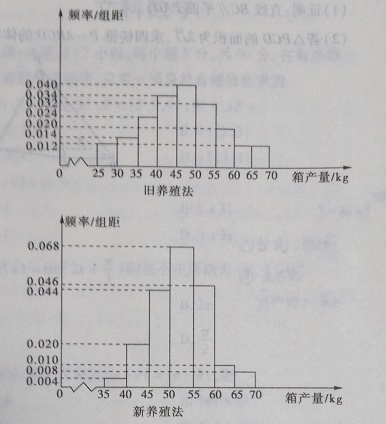
考点：频率分布直方图，众数、中位数、平均数、方差

分析：以上图为例，

• 求众数：

“旧养殖法”的众数为\(47.5\)；“新养殖法”的众数为\(52.5\)；

• 求中位数：

“旧养殖法”的中位数先判断其大概位置，由于\(25-50\)之间的面积和为\(0.62\)，25-45之间的面积和为\(0.42\)，

故中位数一定位于\(45-50\)之间，设中位数为\(x\)，则\(0.42+(x-45)\times0.04=0.50\)，求得\(x=47\)，即中位数为\(47\)。

• 求平均数：比如“旧养殖法”的平均数的计算

\(\bar{x}=27.5\times5\times0.012+32.5\times5\times0.014+37.5\times5\times0.024\)

\(+42.5\times5\times0.034+47.5\times5\times0.040+52.5\times5\times0.032\)

\(+57.5\times5\times0.020+62.5\times5\times0.012+67.5\times5\times0.012\)

\(=47.1\)；

“新养殖法”的平均数的计算

\(\bar{y}=37.5\times5\times0.004+42.5\times5\times0.020+47.5\times5\times0.044\)

\(+52.5\times5\times0.068+57.5\times5\times0.046\)

\(+62.5\times5\times0.010+67.5\times5\times0.008\)

\(=52.35\)；

求方差：比如“新养殖法”的方差计算

\(S^2=(37.5-52.35)^2\times 0.004\times 5+(42.5-52.35)^2\times 0.020\times 5+(47.5-52.35)^2\times 0.044\times 5\)

\(+(52.5-52.35)^2\times 0.068\times 5+(57.5-52.35)^2\times 0.046\times 5\)

\(+(62.5-52.35)^2\times 0.010\times 5+(67.5-52.35)^2\times 0.008\times 5\)

\(=?\)

感悟反思：

1、深入理解频率分布直方图，掌握众数、中位数、平均数、方差的算法；

2、为什么平均数要这样计算？

比如给定数据\(1，2，3，4，5\)的平均数的算法是\(\bar{x}=\cfrac{1+2+3+4+5}{5}=3\)，

那么给定数据\(2，2，4，4，4\)的平均数的算法是

\(\bar{x}=\cfrac{2+2+4+4+4}{5}=\cfrac{2\times 2+4\times 3}{5}\)

\(=2\times \cfrac{2}{5}+4\times \cfrac{3}{5}\)，

表达式中的\(\cfrac{2}{5}\)和\(\cfrac{3}{5}\)的含义就是\(\cfrac{频数}{样本容量}=频率\)。

• 2、利用茎叶图估算平均数、方差

• 3、利用给定数据估算平均数、方差

转载于:https://www.cnblogs.com/wanghai0666/p/6678447.html