Codeforces Beta Round #34 (Div. 2) E. Collisions-优快云博客

本文介绍了一个关于弹性碰撞模拟的问题，通过暴力求解的方式找到每个小球在特定时间后的精确位置。文章详细介绍了碰撞处理的数学原理及算法实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

On a number line there are n balls. At time moment 0 for each ball the following data is known: its coordinate xi, speed vi (possibly, negative) and weight mi. The radius of the balls can be ignored.

The balls collide elastically, i.e. if two balls weighing m1 and m2 and with speeds v1 and v2 collide, their new speeds will be:

$\text{[math]}$ .

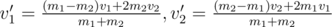
Your task is to find out, where each ball will be t seconds after.

Input

The first line contains two integers n and t (1 ≤ n ≤ 10, 0 ≤ t ≤ 100) — amount of balls and duration of the process. Then follow n lines, each containing three integers: xi, vi, mi (1 ≤ |vi|, mi ≤ 100, |xi| ≤ 100) — coordinate, speed and weight of the ball with index i at time moment 0.

It is guaranteed that no two balls have the same coordinate initially. Also each collision will be a collision of not more than two balls (that is, three or more balls never collide at the same point in all times from segment [0;t]).

Output

Output n numbers — coordinates of the balls t seconds after. Output the numbers accurate to at least 4 digits after the decimal point.

Sample test(s)

input

2 9
3 4 5
0 7 8

output

68.538461538
44.538461538

input

output

-93.666666667
-74.666666667
-15.666666667

因为数据量很少，直接暴力求解即可，细节问题不少，WA了多次。更悲催的是，codeforces上用gun C++编译在test 24出错，但是本机测试答案却无误，用ms 2010编译就AC了。估计是浮点数的精度问题，两种编译器的处理方式有异……

AC Code：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <vector>
#include <queue>
#include <map>
#include <algorithm>
#include <string>

using namespace std;

const double MAXN = 10000000.000000;
const double eps = 10e-6;
const double zero = 0.000000;
vector<int> idx;

int main()
{
    int n;
    double t;
    double x[102], v[102], m[102];
    while(scanf("%d %lf", &n, &t) != EOF)
    {
        for(int i = 0; i < n; i++)
            scanf("%lf %lf %lf", &x[i], &v[i], &m[i]);
        while(fabs(t - zero) > eps)
        {
            double min = t;
            double tmp;
            idx.clear();
            for(int i = 0; i < n; i++)
            {
                for(int j = i + 1; j < n; j++)
                {
                    tmp = MAXN;
                    if(fabs(x[i] - x[j]) < eps) continue;  //两个球碰撞之后的瞬间在同一位置
                    if(v[i] * v[j] > zero)
                    {
                        if(v[j] == v[i]){}
                        else if(x[i] > x[j])
                            tmp = (x[i] - x[j]) / (v[j] - v[i]);
                        else
                            tmp = (x[j] - x[i]) / (v[i] - v[j]);
                    }
                    else
                    {
                        if(v[j] == zero && v[i] == zero){}
                        else if(x[i] > x[j] && v[i] <= zero && v[j] >= zero)
                            tmp = (x[i] - x[j]) / (-v[i] + v[j]);
                        else if(x[i] < x[j] && v[i] >= zero && v[j] <= zero)
                            tmp = (x[j] - x[i]) / (-v[j] + v[i]);
                    }
                    if(tmp > zero && min >= tmp)  //可能有多对球在不同地点同时碰撞，故而min>=tmp而非min>tmp
                    {
                        if(min > tmp)
                        {
                            idx.clear();
                            //当多对球同时碰撞时才需要存储多对下标，不然一定要清空原来
                            //存储的一对下标
                        }
                        min = tmp;
                        idx.push_back(i);
                        idx.push_back(j);
                    }
                }
            }
            t -= min;
            for(int i = 0; i < n; i++)
            {
                x[i] = x[i]  + v[i] * min;
            }
            int i, j;
            for(vector<int>::iterator it = idx.begin(); it != idx.end(); it += 2)
            {
                i = *it, j = *(it + 1);
                double vi = v[i];
                //更新v[j]时需要用到v[i],而v[i]在更新v[j]前已经更新，故而要备份v[i]
                v[i] = ((m[i] - m[j])*v[i] + 2.000000 * m[j]*v[j]) / (m[i] + m[j]);
                v[j] = ((m[j] - m[i])*v[j] + 2.000000 * m[i]*vi) / (m[j] + m[i]);
            }
        }
        for(int i = 0; i < n; i++)
            printf("%.5lf\n", x[i]);
    }
}