Tips

最新推荐文章于 2022-10-24 09:44:35 发布

转载最新推荐文章于 2022-10-24 09:44:35 发布 · 51 阅读

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/radiumlrb/p/5759524.html

1)字符串转换数字

1 if(str[i]>='0'&&str[i]<='9') {
2     int j=0; 
3     do{ 
4         j*=10;j+=int(str[i]-'0'); 
5         i++; 
6     }while(str[i]>='0'&&str[i]<='9');

//实际上为读入优化的一部分

2)进制转换万能模板

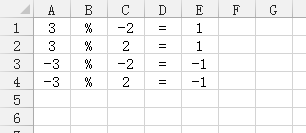
 1 #include <cstdio>
 2 using namespace std;
 3 int x, s, k, i = 0;
 4 char ans[256];
 5 char trans(int x){
 6     return (x < 10) ? (x + '0') : (x - 10 + 'A');
 7 }
 8 int main(){
 9     scanf("%d%d", &x,&k);
10     if(x==0) printf("0");
11     else{
12         while (x){
13                int mod = x % k;
14             mod = (mod < 0) ? (mod - k) : mod;
15             ans[i++] = trans(mod);
16             x = (x - mod) / k;
17         }
18         while (i--) printf("%c", ans[i]);
19     }
20     return 0;
21 }

附几个样例:

3)二维数组前缀和

注意前缀和的求法和面积的表示方法，对于二维数组的前缀和，先像一维数组那样求一遍每行的前缀和，再将每一个前缀和加上自己上面的点的前缀和。

而面积的表示：对于i,j点边长为l的正方形，前缀和表示：sum[i][j]-sum[i-l][j]-sum[i][j-l]+sum[i-l][j-l]

栗子：http://www.cnblogs.com/radiumlrb/p/5808285.html

http://www.cnblogs.com/radiumlrb/p/5808527.html

4)关于C标准下字符串输入的问题//2018-09-25

scanf接收字符时的格式是scanf("%c",&ch)(ch是定义过的接收键盘输入字符的变量，下同);。这种格式下，无论输入缓冲区里有多少字符，scanf("%c",&ch);都只接收最前面的一个赋给ch，但系统要以'\n'作为输入结束的命令，那么scanf("%c",&ch);在接收一个输入字符时必然会把'\n'遗留在缓冲区里。

这样问题就来了，由于'\n'也是一个字符，所以下一个scanf("%c",&ch2);就会把上一个scanf("%c",&ch);遗留在缓冲区里的'\n'接收并赋给ch2，这就造成第二个scanf("%c",&ch2);失去了从键盘接收用户输入的字符的机会(scanf("%c",&ch2)只接收一个字符)，从而造成代码运行出错。

解决办法很多，在scanf("%c",&ch);语句前加getchar();，加fflush(stdin);，甚至把scanf("%c",&ch);写两遍都能凑效。但这不仅要消费空间时间，而且阅读也不直观。其实知道了原理解决起来就方便了，最简单的办法是把每一个类似scanf("%c",&ch);这样读字符的语句改写成scanf(" %c",&ch)(%前有个空格);就可以了，原理是这个空格会命令scanf跳过所有的广义空格(' '、'\t'、'\n'等)再接收字符——当然没有空格就不会有跳过动作——问题就迎刃而解了。

下面提供验证代码：

//#include "stdafx.h"//If the vc++6.0, with this line.
#include "stdio.h"
int main(void){
    char a,b;
    scanf(" %c",&a);
    scanf(" %c",&b);
    printf("%c %c\n",a,b);
    return 0;
}

5)循环中不要放置strlen等函数

惨痛的教训

strlen所作的仅仅是一个计数器的工作，它从内存的某个位置（可以是字符串开头，中间某个位置，甚至是某个不确定的内存区域）开始扫描，直到碰到第一个字符串结束符'\0'为止，然后返回计数器值(长度不包含'\0')。

我们用cin>>s和scanf(%s)输入字符串时，会在接受完字符串后在末尾加个'\0'，也就是NULL作为字符串结束符。

所以用strlen函数求解字符串长度的时候，复杂度就是O(n)。如果在循环中用

for (int i = 0; i < strlen(s); ++i)//复杂度O(n2)
那就麻烦了，可能会超时，解决办法：

（1）先把strlen(s)用变量存储起来，再放入循环中；

（2）或者用s[i] != '\0'；

（3）或者用string s存储，用s.size();

做poj1152的时候发现用i < s.size()和i < strlen(s)最终用时差不多。但是最好还是用前两种。

2.类似的还有sqrt函数
循环的时候要么先算出sqrt(x)，要么就用i*i < x，最好不要用i < sqrt(x)，增加复杂度。

其他的类似。

6)数组开大点不花钱，开小了会抓狂

3kw个int自己把握好

极限空间的题目:http://www.cnblogs.com/radiumlrb/p/5836629.html

7)素数筛法

普通的线性筛法：

#include"cstdio"
#include"cstring"
using namespace std;
#define MAX 100000//求MAX范围内的素数
long long su[MAX],cnt;
bool isprime[MAX];
void prime()
{
    cnt=1;
    memset(isprime,1,sizeof(isprime));//初始化认为所有数都为素数
    isprime[0]=isprime[1]=0;//0和1不是素数
    for(long long i=2;i<=MAX;i++)
    {
        if(isprime[i])//保存素数
        {
            su[cnt++]=i;
        }
        for(long long j=i*2;j<=MAX;j+=i)//素数的倍数都为合数
        {
            isprime[j]=0;
        }
    }
}
int main()
{
    prime();
    for(long long i=1;i<cnt;i++)
        printf("%d  ",su[i]);
    return 0;
}

优化后的线性筛法：

#include"cstdio"
#include"cstring"
using namespace std;
#define MAX 100000//求MAX范围内的素数
long long su[MAX],cnt;
bool isprime[MAX];
void prime()
{
    cnt=1;
    memset(isprime,1,sizeof(isprime));//初始化认为所有数都为素数
    isprime[0]=isprime[1]=0;//0和1不是素数
    for(long long i=2;i<=MAX;i++)
    {
        if(isprime[i])
            su[cnt++]=i;//保存素数i
        for(long long j=1;j<cnt&&su[j]*i<MAX;j++)
        {
            isprime[su[j]*i]=0;//筛掉小于等于i的素数和i的积构成的合数
        }
    }
}
int main()
{
    prime();
    for(long long i=1;i<cnt;i++)
        printf("%d  ",su[i]);
    return 0;
}

普通的线性筛法虽然大大缩短了求素数的时间，但是实际上还是做了许多重复运算，比如2*3=6，在素数2的时候筛选了一遍，在素数为3时又筛选了一遍。如果只筛选小于等于素数i的素数与i的乘积，既不会造成重复筛选，又不会遗漏。时间复杂度几乎是线性的。

转载于:https://www.cnblogs.com/radiumlrb/p/5759524.html