支持向量机

最新推荐文章于 2022-10-07 12:29:08 发布

转载最新推荐文章于 2022-10-07 12:29:08 发布 · 100 阅读

1 ·

CC 4.0 BY-SA版权

原文链接：http://www.cnblogs.com/niniya/p/8848541.html

1、SVM原理

SVM是一种二类分类模型，其基本模型定义为特征空间上的间隔最大的线性分类器。工作原理是一个支持向量机构造一个超平面，可用于分类、回归。

（1）当训练样本线性可分时，通过硬间隔最大化，学习一个线性分类器，即线性可分支持向量机；

（2）当训练数据近似线性可分时，引入松弛变量，通过软间隔最大化，学习一个线性分类器，即线性支持向量机；

（3）当训练数据线性不可分时，通过使用核技巧及软间隔最大化，学习非线性支持向量机。

当样本在原始空间线性不可分时，使用核函数将样本从原始空间映射到一个更高维的特征空间，在更高的维度上找到超平面，得到超平面方程，更高的这个维度只是像在解几何问题里使用的辅助线一样，最后得到的方程不会增加其他维度。常用的核函数有线性核函数、多项式核函数、径向核基函数、高斯核函数等。

2、python 中实现支持向量机使用SVC

参数：

C：惩罚参数，默认值是1.0。C越大，相当于惩罚松弛变量，希望松弛变量接近0，即对误分类的惩罚增大，趋向于对训练集全分对的情况，这样对训练集测试时准确率很高，但泛化能力弱。C值小，对误分类的惩罚减小，允许容错，将他们当成噪声点，泛化能力较强。

kernel ：核函数，默认是rbf，可以是‘linear’（线性核函数）, ‘poly’（多项式核函数）, ‘rbf’（径向基核函数）, ‘sigmoid’（神经元激活核函数）, ‘precomputed’ （自定义核函数）。

degree ：多项式poly函数的维度，默认是3，选择其他核函数时会被忽略。

gamma ： ‘rbf’,‘poly’ 和‘sigmoid’的核函数参数。默认是’auto’，则会选择1/n_features

coef0 ：核函数的常数项。对于‘poly’和 ‘sigmoid’有用。

probability ：是否采用概率估计，默认为False

shrinking ：是否采用shrinking heuristic方法，默认为true

tol ：停止训练的误差值大小，默认为1e-3

cache_size ：核函数cache缓存大小，默认为200

class_weight ：类别的权重，字典形式传递。设置第几类的参数C为weight*C(C-SVC中的C)

verbose ：允许冗余输出

max_iter ：最大迭代次数。-1为无限制。

decision_function_shape ：可选值‘ovo’, ‘ovr’ ，默认‘ovr’，多分类时的处理方法。ovo一对一，ovr一对多。

random_state ：数据洗牌时的种子值，int值。

3、SVM处理多分类

两种方法：

直接法：直接在目标函数上修改，将多个分类面的参数求解合并到一个最优化问题里面。

间接法：对训练器进行组合，其中比较典型的有一对一，和一对多

（1）一对多：依次把某个类别的样本归为一类,其他剩余的样本归为另一类，这样k个类别的样本就构造出了k个SVM。分类时将未知样本分类为具有最大分类函数值的那类。

（2）一对一：在任意两类样本之间设计一个SVM，因此k个类别的样本就需要设计k(k-1)/2个SVM。当对一个未知样本进行分类时，最后得票最多的类别即为该未知样本的类别。

#导入库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
from  sklearn.svm import SVC
from sklearn import datasets
from sklearn.cross_validation import train_test_split  #用于数据集划分
from sklearn.preprocessing import StandardScaler

#获取数据
iris=datasets.load_iris()
x=iris.data[:,[2,3]]
y=iris.target

#将数据分为训练集、测试集
x_train,x_test,y_train,y_test=train_test_split(x,y,test_size=0.3,random_state=0)

#对数据进行标准化处理
sc=StandardScaler()  #实例化一个StandardScaler对象
sc.fit(x_train) #计算x_train每个特征的均值和标准差
x_train_std=sc.transform(x_train)    
x_test_std=sc.transform(x_test)

#建立SVM模型
svm=SVC(kernel='linear',C=0.1,random_state=0)
svm.fit(x_train_std,y_train)

#应用SVM模型
pre_targets=svm.predict(x_test)

#构建一个函数，用于svm可视化
def plot_decision_regions(x,y,classifier,test_idx=None, resolution=0.02):
    markers=('s','x','o','^','v')
    colors=('red','blue','lightgreen','gray','cyan')
    cmap=ListedColormap(colors[:len(np.unique(y))])  #一个颜色列表，

#做网格数据，用于类别颜色分区
    x1_min,x1_max=x[:,0].min()-1,x[:,0].max()+1
    x2_min,x2_max=x[:,1].min()-1,x[:,1].max()+1
    xx1,xx2=np.meshgrid(np.arange(x1_min,x2_max,resolution),np.arange(x2_min,x2_max,resolution))#resolution=0.02,指步长
    z=classifier.predict(np.array([xx1.ravel(),xx2.ravel()]).T)
    z=z.reshape(xx1.shape)
    plt.contourf(xx1,xx2,z,alpha=0.4,cmap=cmap) #xx1、xx2为网格点数据，z为网格点对应的高度
    plt.xlim(xx1.min(),xx1.max())  #x轴刻度范围
    plt.ylim(xx2.min(),xx2.max())  #y轴刻度范围

    #对所有样本做散点图for idx,cl in enumerate(np.unique(y)):
        plt.scatter(x=x[y==cl,0],y=x[y==cl,1],alpha=0.8,c=cmap(idx),marker=markers[idx],label=cl)

 #对测试集样本做散点图
    if test_idx:
        x_test,y_test=x[test_idx,:],y[test_idx]
        plt.scatter(x_test[:,0],x_test[:,1],c='Cyan',alpha=0.8,linewidth=1,marker='o',s=55,label='test set')

#可视化
x_combined_std=np.vstack((x_train_std,x_test_std))
y_combined=np.hstack((y_train,y_test))
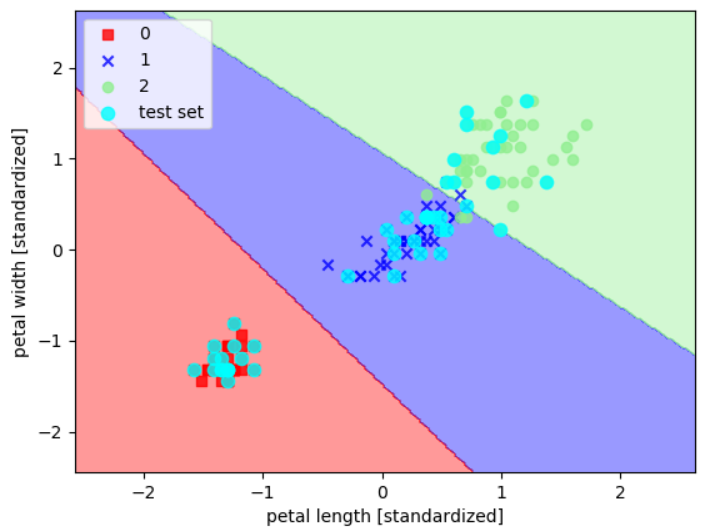
plot_decision_regions(x_combined_std,y_combined,classifier=svm,test_idx=range(105,150)) #test_idx是测试集的数量45个，训练集和测试集拼接后，测试集排后面即105~150为测试集
plt.xlabel('petal length [standardized]')
plt.ylabel('petal width [standardized]')
plt.legend(loc='best')
plt.show()