面向对象第一次总结

前言

这三次作业都是关于多项式求导的问题，不过难度逐步递进，而且在第三次作业里面加入了嵌套。在前两次作业中，多项式中的每一项因子确定，所以完成这部分代码是不太难的，主要是在优化输出多项式长度上面下功夫；而第三次作业由于存在嵌套，原来的结构不太好扩展，而且读入、解析上也有很大的改变，所以第三次作业单独拿出来说。

第一、二次作业

代码度量

第一次作业事实上只写了一个类，如下图所示：

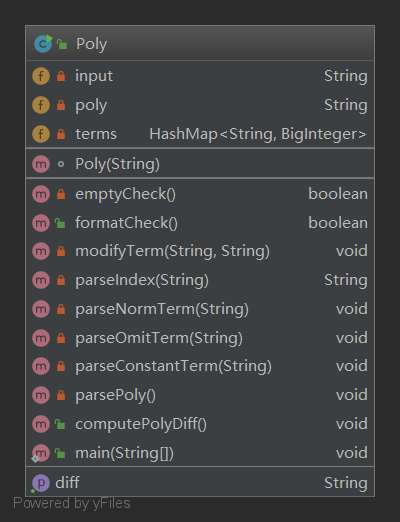
多项式的格式检查、解析、求导都在一个类中实现，总共代码200多行，下面是各个方法的复杂度分析：

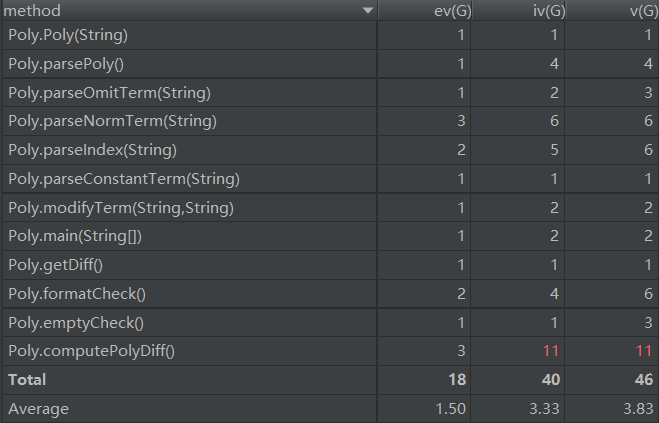
其中多项式求导复杂度有点高，主要是在优化上的处理有一些分支，其实可以再分一个对项求导的函数出来，可以把函数的结构变得再简单一点。在第二次作业中，我把多项式的求导函数剥离出来，单独做了一个多项式计算的类，这样原来多项式的类只需要关注多项式解析和存储，计算交给其他类来处理。第二次作业加入了三角函数，代码在400行左右，依赖关系如下：

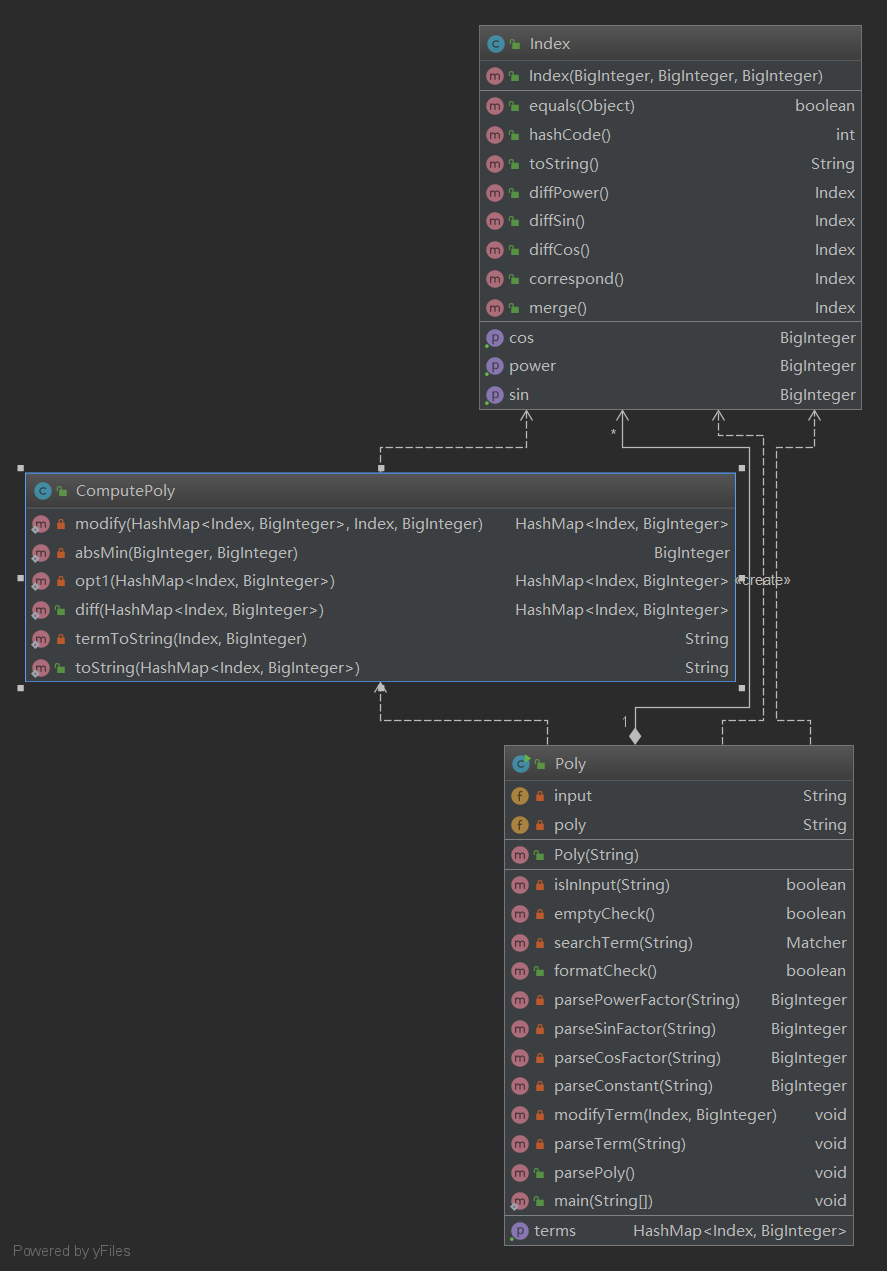
 其中Poly是多项式类，用于解析、存储多项式，ComputePoly用于多项式求导。各方法的复杂度如下所示：

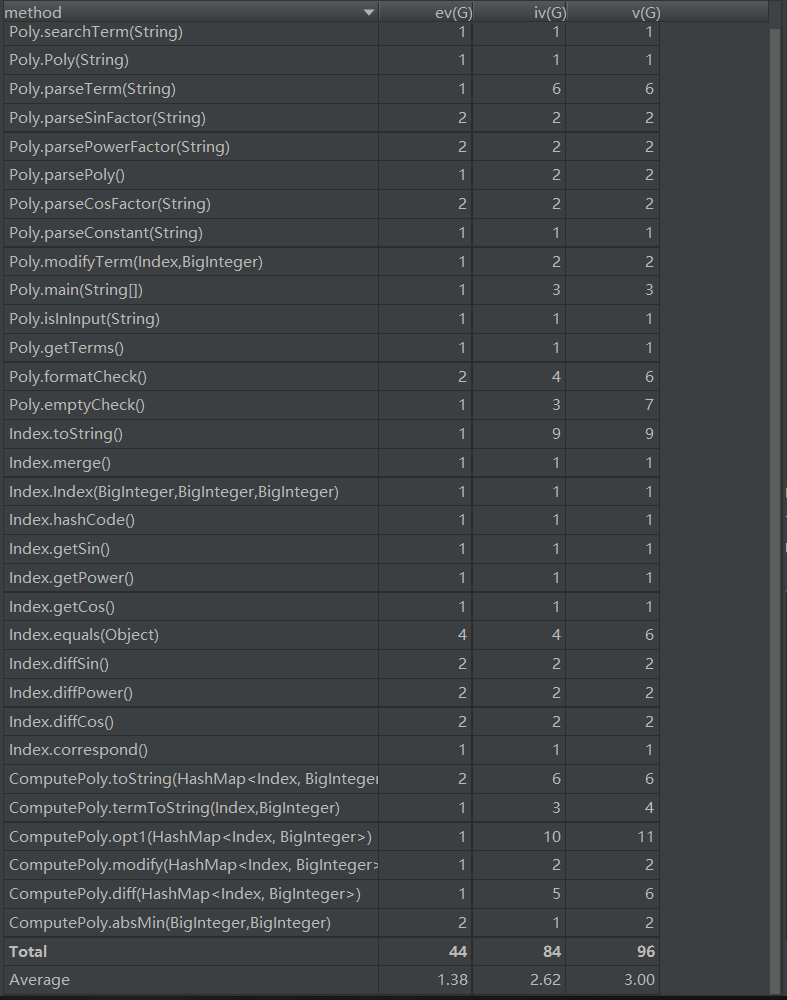
由于多项式中加入了三角函数，以及求导法则的缘故，函数增加了很多，但是基本思路和第一次作业一致。

思路分析

前两次作业由于多项式每一项的元素固定，每一项的形式比较简单，只需要几个指数和一个系数就可以表示，所以采用正则表达式读入、解析，HashMap存储多项式，方便合并同类项。

多项式解析

在前两次作业中，我采用正则表达式来解析输入，由于一次性判断整个多项式是否合法存在爆栈的风险，所以我才用单次匹配一项，循环匹配直到不能匹配到新的项为止。

在匹配之前，我先检查空白字符是否符合要求，然后删去所有空白字符。这样在接下来每一项的匹配中就不需要考虑空白字符的位置，简化正则。除了第一项，每一项前面至少一个正负号，所以我在处理输入串的时候，判断了一下第一个非空白字符是否为正负号，如果没有就添加一个正号，使得每一项都有统一的格式，接下来只需要逐项匹配即可。同时匹配上一项就删去该项，如果该输入串符合要求，匹配结束后，字符串应该为空串。

在项的解析中，首先解析每一个因子，比如幂函数、三角函数等，最后再解析有符号整数。先匹配有符号整数有可能导致指数部分先匹配上，发生解析错误，然后根据各因子的指数，存到HashMap的相应位置。

多项式求导

在多项式求导中，我是对各个因子进行求导，然后将结果加入到新的HashMap中，最后将HashMap转成字符串输出即可。在优化部分，除了对于系数、指数的特殊处理，还有正负项位置的问题，如果正项为首项，那么可以去掉一个正号。

思路总结

总的来说，代码可以分为三个部分，解析、求导和优化。在解析部分，正则的作用可以说是非常的大，求导和优化就因人而异了，这里使用的HashMap很方便去查找项，包括但不限于合并同类项以及三角函数合并。

bug分析

我在这部分出现的bug主要包括，省略形式的正负号个数、输入串是否为空等。空串的判断可以用Scanner类的hasNextLine来判断，省略形式的正负号需要对题目有较好的理解。对于大数的处理可以直接用BigInteger类。在第二次优化部分，由于不能在循环中增删HashMap，所以需要分别构造增删队列，在遍历结束后用于增删。

第三次作业

代码度量

第三次作业由于加入了嵌套，java的正则好像不能很好支持，而且项的形式也较为复杂，于是只能像上学期一样吭哧吭哧写了个“编译器前端”，用于解析输入串，然后使用树状结构去存储整个表达式，最后调用求导即可，具体依赖关系如下：

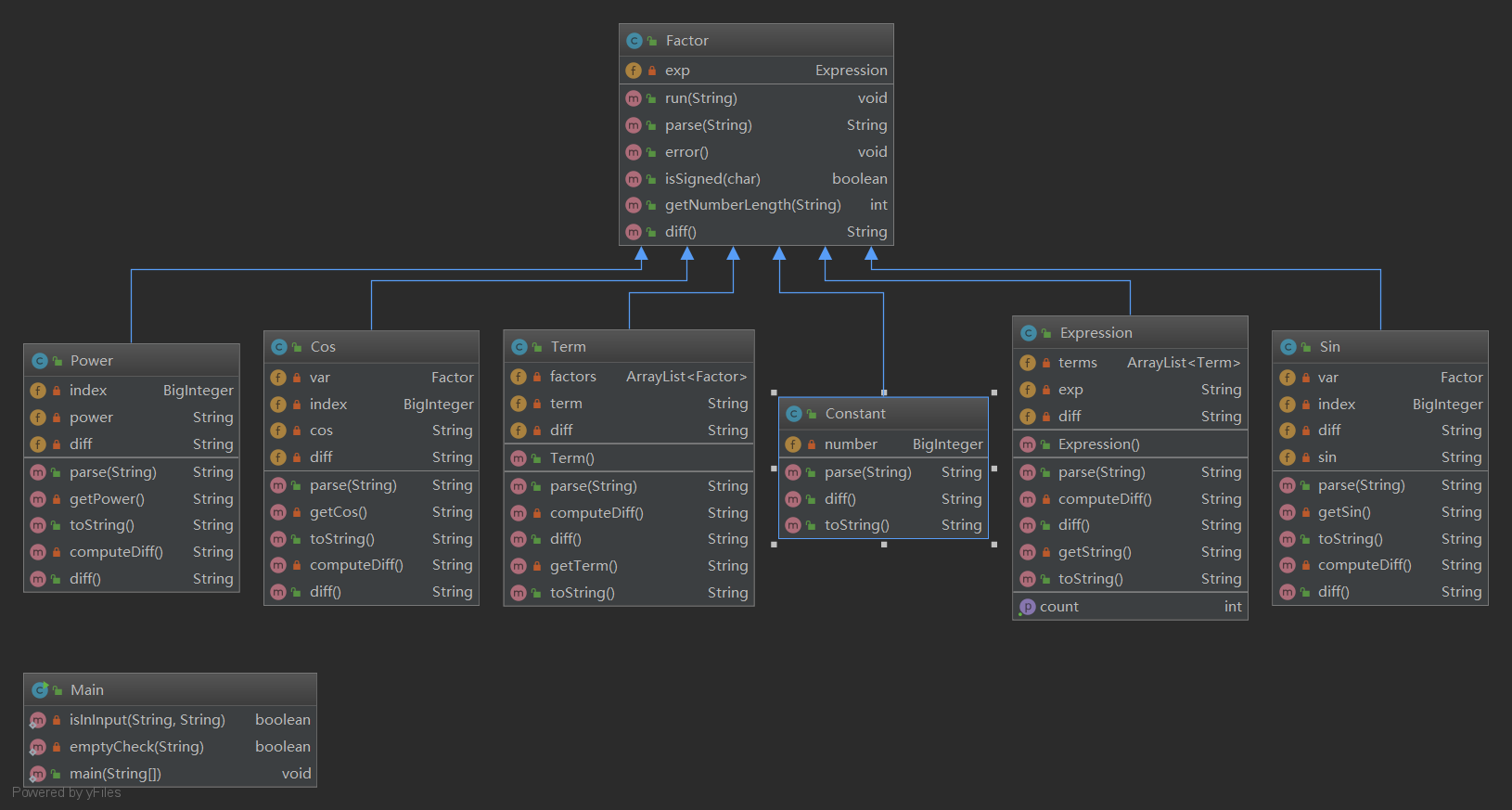
我在三角函数加入了Factor自变量的位置，用于嵌套，然后对于该三角函数的求导可以套用求导法则得出。整个代码700行左右，找bug可以说是有点酸爽了。

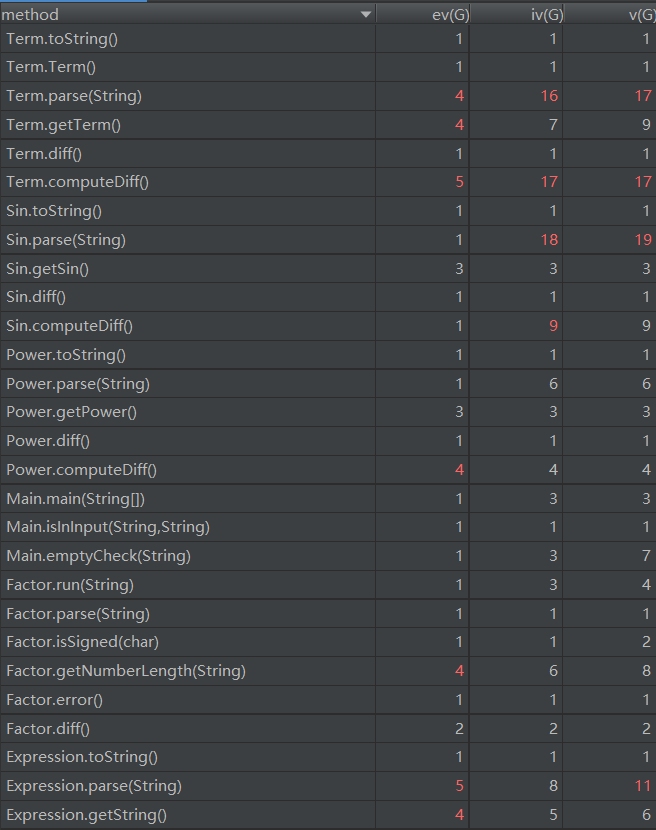
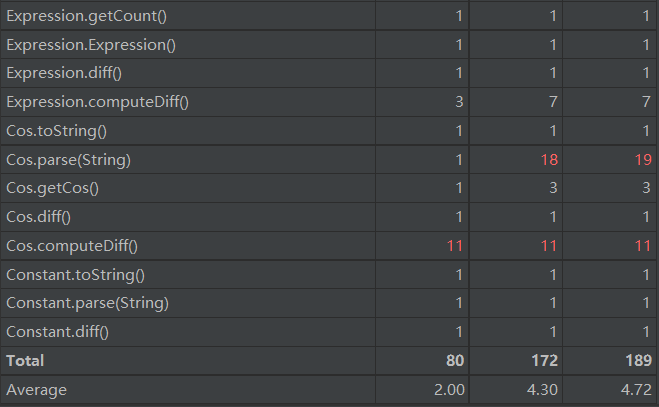
这里面由于优化等因素，导致复杂度函数的复杂度较大。

思路分析

多项式解析

这部分，经过一晚上的奋斗，我发现我还是要放弃正则，改用编译器写法，将表达式分为expression-term-factor三层，其中(expression)也可以为factor，然后逐层解析，边验证合法性边构造树状图。在返回最后一层expression时，应该没有待解析的字符串了。

在解析之前，首先检查空白字符的合法性，然后去掉所有的空白字符。在解析的过程中，对可能出现的情况创建if分支，对不满足所有if的分支，进行错误处理，然后递归调用。在三角函数内部，由于存在嵌套，所以用factor来作为自变量，先解析嵌套因子，然后创建对应的子类继续解析。

在解析完成后，进行求导，并将结果存储下来。因为在term中使用ArrayList存储，在求导的过程中存在对一项多次求获取字符串和求导，这样可以降低一部分的复杂度，同时在debug过程中也可以查看各项的求导结果。

 多项式求导

多项式求导倒是比较形式化，主要是利用求导规则即可，但是如果要优化的话，那么需要创建很多分支去特殊处理。除此之外，对项的求导，往往会有多个项，那么需要对这多个项加括号，保证计算正确，但是对长度的优化稍有不便。

bug分析

在第三次作业中，主要出现的bug主要出现在解析多项式和对多项式求导中。在解析多项式，由于使用“编译器”的模式，所以需要对各种可能存在的情况进行判断，稍有考虑不慎，就会有越界的可能性，或者误报错误。在对多项式的求导中，由于三角函数中存在指数，对于各个指数的优化，很容易写错求导公式。除此之外，对term进行求导时，有可能会出现多个项相加的情况，那么需要加个括号来保证整体性，不然可能在嵌套结构中出错，比如对于“sin((sin(x)*sin(x)))”的求导。而且对于term类而言，并不需要继承factor类，虽然并没有在代码中使用，但还算是一个小瑕疵。

具体重构

如果需要重构的话，那么我会针对优化进行重构，重写equals函数使得各个term表达式可以互相合并。但是对于三角函数合并还是没有太好的想法，在我的思路中，需要对每个项进行遍历，寻找可以合并的项，但是目前使用ArrayList存储，如果强行合并，那么复杂度可能会比较大，可能还是需要使用hashCode函数。

作业感想

这三次作业的难度是逐渐上升的，前两次作业联系较为紧密，而且思路也比较直，基本上网上查查资料，写写就完了。第三次作业由于嵌套的问题，必须使用新的代码结构，所以花的时间会比较长。其实如果老师在第一周就和我们说最终的目标的话，那在前两次作业中，我们就会进行相关的设计，那么第二次和第三次的代码结构也许用的一样，会让我们有更多的时间去考虑优化的问题。

这三次作业下来，基本上熟悉Java的常用容器和一些常规操作，并且对类和继承有了初步的认识。接下来要对多线程进行学习，免得后面手忙脚乱。

转载于:https://www.cnblogs.com/Tywin/p/10597203.html