原码、反码、补码

转载于 2025-05-31 11:58:06 发布 · 90 阅读

在计算机中， 原码、反码、补码 是表示有符号整数的三种方式，主要用于解决 负数存储和运算 的问题。它们的定义、作用及使用场景如下：

Java 大端、小端存储，short、int 转 byte数组，& 0xFF 清除高位符号扩展，保留低 8 位。

1. 原码（Sign-Magnitude）

定义

最高位表示符号（0 为正，1 为负），其余位表示数值。
例如，8 位二进制：
- +5 的原码：0000 0101
- -5 的原码：1000 0101

特点

直观，人类容易理解。
问题：
- +0 和 -0 不唯一（0000 0000 和 1000 0000）。
- 加减运算复杂，需要额外判断符号位。

使用场景

早期计算机（如 IBM 701）使用原码，但现代计算机基本不再使用。

2. 反码（Ones' Complement）

定义

正数：反码 = 原码。
负数：符号位不变，其余位 按位取反。
例如：
- +5 的反码：0000 0101（同原码）
- -5 的反码：1111 1010（符号位 1，数值位取反）

特点

解决了 +0 和 -0 的问题（反码下 -0 是 1111 1111，但仍有冗余）。
缺点：
- 加减运算仍需处理进位（如 -5 + 5 = 1111 1010 + 0000 0101 = 1111 1111，即 -0）。
- 硬件实现复杂。

使用场景

早期计算机（如 PDP-1）使用反码，但已被补码取代。

3. 补码（Two's Complement）

定义

正数：补码 = 原码。
负数：反码 + 1（即 取反后加 1）。

例如：

+5 的补码：0000 0101（同原码）

-5 的补码：

原码：1000 0101
反码：1111 1010
补码：1111 1011 （反码 + 1）

特点

解决了 +0 和 -0 问题（补码下 -0 表示为 0000 0000，与 +0 相同）。
加减运算统一（直接按二进制加法计算，无需额外处理符号位）。
硬件实现简单（只需加法器，无需额外电路）。

使用场景

现代计算机（包括 Java）全部使用补码存储有符号整数。
例如：
- Java 的 byte、short、int、long 均用补码表示。
- 0xFC（1111 1100）在 byte 类型中表示 -4（因为补码计算：~1111 1100 + 1 = 0000 0100，即 -4）。

4. 为什么需要反码和补码？

（1）解决 `+0` 和 `-0` 问题

原码和反码中，+0 和 -0 的表示不同，导致比较和运算复杂。
补码中 0 只有一种表示（0000 0000），简化逻辑。

（2）统一加减运算

补码下，减法可以转换为加法（A - B = A + (-B)），硬件只需加法器。

例如：5 - 3 = 5 + (-3)：

5 的补码：0000 0101
-3 的补码：1111 1101
相加：0000 0101 + 1111 1101 = 0000 0010 （即 2）

（3）硬件优化

补码运算无需额外判断符号位，减少电路复杂度。

5. 实际应用示例

（1）Java 中的 `byte` 类型

byte b = (byte) 0xFC; // 0xFC = 1111 1100（补码）
System.out.println(b); // 输出 -4（因为补码 1111 1100 表示 -4）

（2）无符号转换

由于 Java 没有无符号 byte，需用 & 0xFF 转换：

int unsignedValue = b & 0xFF; // 0xFC（252）
System.out.println(unsignedValue); // 输出 252

（3）网络协议 & 文件解析

读取 TCP/IP 报文、二进制文件时，数据可能是补码形式，需按补码解析：

// 从文件读取 2 字节的 short（补码存储）
short value = (short) ((bytes[0] << 8) | (bytes[1] & 0xFF));

6. 总结

表示方式	定义	优点	缺点	使用场景
原码	符号位 + 绝对值	直观	`±0` 问题，运算复杂	早期计算机
反码	负数：符号位 + 取反	解决 `±0` 问题	运算仍有进位问题	过渡方案（如 PDP-1）
补码	负数：反码 + 1	统一加减法，硬件简单	无	现代计算机（Java/C/C++）

补码是现代计算机的标准选择，因其运算高效、硬件友好。理解补码是处理二进制数据、网络协议、文件解析的基础。

示例

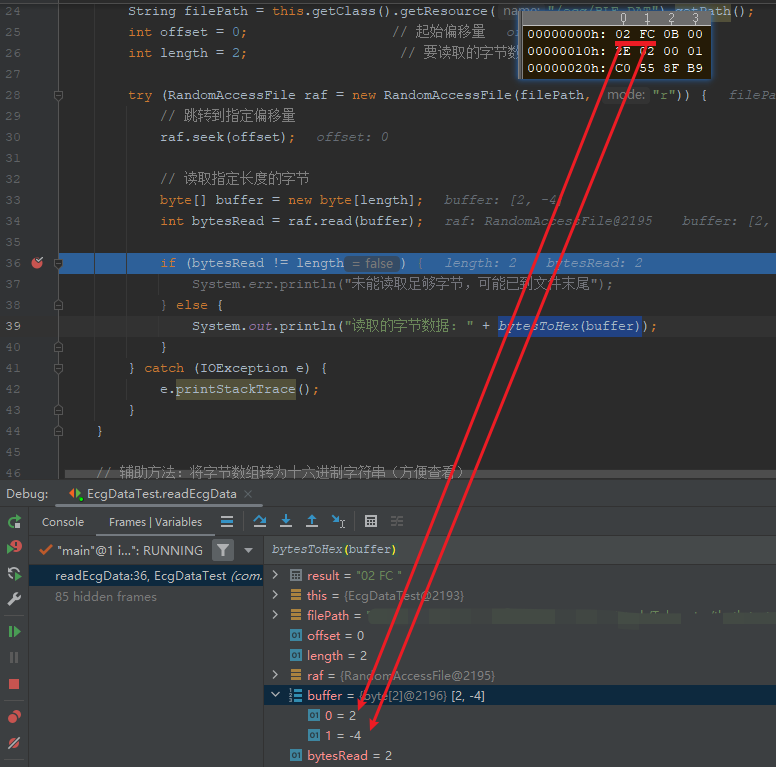
在 Java 中，byte 类型是 有符号的 8 位整数，现代计算机（包括 Java）全部使用补码存储有符号整数，第一位为符号位，取值范围是 10000000 ~ 01111111，即：-128 到 127 （即 0x80 到 0x7F）。
0xFC（二进制 1111 1100）到 byte 变量时，Java 会将其解释为 有符号的补码（two's complement），因此 0xFC 会被视为 -4。

为什么在Java中 `0xFC` 变成 `-4`？

byte 是有符号的：
- 0xFC（二进制 1111 1100）的最高位是 1，表示它是一个负数。
- Java 使用 补码（two's complement） 表示负数。
补码转十进制：
- 补码的规则：负数值 = 原码取反 + 1。
- 0xFC（1111 1100）是某个负数的补码，计算它的原码：
```
补码: 1111 1100 (0xFC)
取反: 1000 0011
+1  : 1000 0100 (结果是 -4)
```
- 因此，0xFC 表示 -4。

示例代码

byte b = (byte) 0xFC; // 0xFC 被强制转换为 byte 类型
System.out.println(b); // 输出 -4
System.out.println(Integer.toHexString(b & 0xFF)); // 输出 "fc"（正确显示无符号值）

如何正确查看 `0xFC`？

如果你希望在调试或打印时看到 0xFC 而不是 -4，可以：

用 & 0xFF 转为无符号 int：

byte b = (byte) 0xFC; // 0xFC 被强制转换为 byte 类型
int unsignedValue = b & 0xFF; // 0xFC (252)
System.out.println(unsignedValue); // 输出 252
System.out.println(Integer.toHexString(unsignedValue)); // 输出 "fc"

& 0xFF 的作用是清除高位符号扩展，保留低 8 位。 https://www.cnblogs.com/vipsoft/p/16241685.html

使用 Byte.toUnsignedInt()（Java 8+）：

byte b = (byte) 0xFC; // 0xFC 被强制转换为 byte 类型
int unsignedValue = Byte.toUnsignedInt(b); // 252

关键点总结

表示方式	值（十进制）	说明
`0xFC`（原始值）	-4	Java `byte` 是有符号的，`0xFC` 是 `-4` 的补码
`b & 0xFF`	252	转为无符号整数，正确显示 `0xFC`
`Byte.toUnsignedInt(b)`	252	Java 8 提供的无符号转换方法