matlab zero padding,二维卷积详解，zero padding 和shape=full, same, valid详解-优快云博客

本文详细探讨了传统离散信号处理中卷积维度的计算，以及Matlab、TensorFlow和PyTorch中卷积函数中padding设置对输出维度的影响。通过对比和实证，揭示了shape、padding选项在卷积操作中的作用与计算公式的关系。

本文主要解释： (1)传统离散信号处理中的卷积维度 L = M+N -1；(2)matlab 卷积函数中的shape=full, same, valid所导致的不同卷积输出维度，和tensorflow的tf.nn.conv2d中的padding=same,valid 导致的不同输出维度；(3) pytorch中的卷积函数中设置的 padding以及torch官方给的卷积的shape计算公式

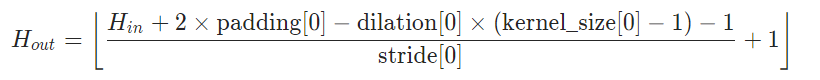
本文主要解释这三者在计算二维卷积输出维度时的差别与联系。不想看推导您可以翻到最后直接看结论。

——————————————————————————————————————————————————

首先来将传统的离散信号处理，大多数人在学信号与系统或者数字信号处理的时候，在学离散卷积的时候，肯定都学过：如果输入的两个离散序列长度分别是M和N，那么他们卷积之后得到的离散序列长度 L=M + N -1。对于二维卷积，输入矩阵P×Q 和 M×N；卷积之后的矩阵 W×H，在两个维度方向上都满足上述公式：W = P+M-1；H = Q+N-1.

有信号处理背景的同学，在初次接触pytorch的卷积及其维度公式时，大多会感觉，怎么本来卷积的维度 L=M + N - 1，在这里就变得这么复杂了：

上图中的公式，stride是指卷积时卷积核移动的步长，dilation是指卷积核元素间的距离，传统信号处理的卷积中stride=1，dilation=1，上图公式简化下来，就是H_out = H_in +2×padding - kernel_size +1；H_in对应M，kernel_size 对应N；一边是加N一边是减kernel_size 看起来似乎有些矛盾，另一个没考虑到的是padding，如果令padding=kernel_size -1，那么两个公式就一样了。