题目所在试卷参考答案:
普通高中招生统一考试
数学试题参考答案及评分意见
一、选择题:(每小题4分,共48分)
CCBAD,CCABD,BC
二、填空题:(每小题4分,共32分)
13、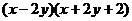 14、
14、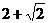 15、990 16、-1
15、990 16、-1
17、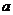 ≥3 18、2 19、2 20、
≥3 18、2 19、2 20、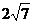
三、解答题:(每小题12分,共48分)(除23小题外,其余各题的评分均为累计计分)
21、解:将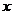 =3代入原方程得:
=3代入原方程得: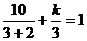 (1分)
(1分)
解得: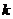 =-3 (4分)
=-3 (4分)
将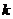 =-3代入原方程得:
=-3代入原方程得: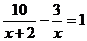 (5分)
(5分)
整理得: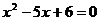 (8分)
(8分)
解得: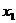 =2,
=2,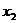 =3 (10分)
=3 (10分)
经检验: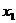 =2,
=2,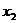 =3都是原方程的解。 (11分)
=3都是原方程的解。 (11分)
∴当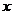 =3是方程的一个根时,
=3是方程的一个根时,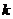 =-3,方程的另一个根为
=-3,方程的另一个根为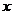 =2 (12分)
=2 (12分)
22、解:(1)设平均每分钟一道正门可以通过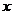 名学生,一道侧门可以通过
名学生,一道侧门可以通过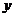 名学生,(1分)由题意得:
名学生,(1分)由题意得:
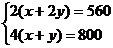 (4分)
(4分)
解得: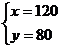 (7分)
(7分)
答:平均每分钟一道正门可以通过120名学生,一道侧门可以通过80名学生。(8分)
(2)这栋楼最多有学生4×8×45=1440(名)
拥挤时5分钟4道门能通过: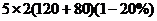 =1600(名)(10分)
=1600(名)(10分)
∵1600>1440
∴建造的4道门符合安全规定。 (12分)
23、(1)(共6分)①7(2分);②26(1分);③5月11至5月29日每天新增确诊病例人数(2分)19(1分)
(2)(共6分)每空位或每空格1分
①10人;②11、40、0.125、0.325;③25;
24、(1)证明:连结AB (1分)
∵四边形AEPB是⊙O1的内接四边形
∴∠ABC=∠E (2分)
在⊙O2中,∠ABC=∠ADC
∴∠ADC=∠E (4分)
又∵AE∥CN
∴∠ADC=∠PAE
故∠PAE=∠E
∴PA=PE (6分)


(2)连结AN (7分)
四边形ANPB是⊙O1的内接四边形
∴∠ABC=∠PNA (8分)
由(1)可知∴∠PDN=∠ADC=∠ABC
∴∠PDN=∠PNA
又∠DPN=∠NPA
∴△PDN∽△PNA (10分)
∴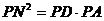 (11分)
(11分)
又∵在⊙O2中,由割线定理:PB.PC=PD.PA
∴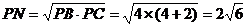 (12分)
(12分)
四、解答题:(共22分)
25、解:(1)由题意得: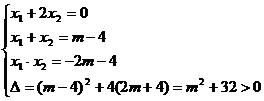
由①②得: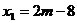 ,
,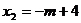
将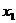 、
、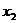 代入③得:
代入③得: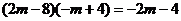
整理得: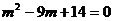
∴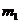 =2
=2 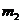 =7 (2分)
=7 (2分)
∵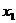 <
<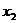
∴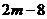 <
<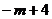
∴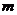 <4
<4
∴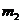 =7(舍去) (3分)
=7(舍去) (3分)
∴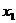 =-4,
=-4,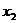 =2,点C的纵坐标为:
=2,点C的纵坐标为: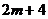 =8
=8
∴A、B、C三点的坐标分别是A(-4,0)、B(2,0)、C(0,8) (4分)
又∵点A与点D关于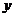 轴对称
轴对称
∴D(4,0) (5分)
设经过C、B、D的抛物线的解析式为: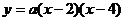 (6分)
(6分)
将C(0,8)代入上式得: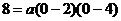
∴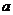 =1
=1
∴所求抛物线的解析式为: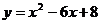 (7分)
(7分)
(2)∵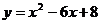 =
=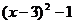
∴顶点P(3,-1) (8分)
设点H的坐标为H(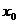 ,
,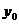 )
)
∵△BCD与△HBD的面积相等
∴∣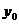 ∣=8
∣=8
∵点H只能在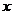 轴的上方,故
轴的上方,故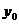 =8
=8
将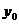 =8代入
=8代入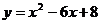 中得:
中得: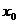 =6或
=6或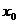 =0(舍去)
=0(舍去)
∴H(6,8) (9分)
设直线PH的解析式为: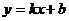 则
则
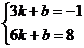 (10分)
(10分)
解得: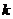 =3
=3 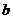 =-10
=-10
∴直线PH的解析式为: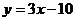 (12分)
(12分)
26、答:可以切割出66个小正方形。 (1分)
方法一:
(1)我们把10个小正方形排成一排,看成一个长条形的矩形,这个矩形刚好能放入直径为10.05cm 的圆内,如图中矩形ABCD。
∵AB=1 BC=10
∴对角线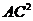 =100+1=101<
=100+1=101<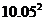 (3分)
(3分)
(2)我们在矩形ABCD的上方和下方可以分别放入9个小正方形。

∵新加入的两排小正方形连同ABCD的一部分可看成矩形EFGH,矩形EFGH的长为9,高为3,对角线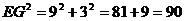 <
<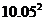 。但是新加入的这两排小正方形不能是每排10个,因为:
。但是新加入的这两排小正方形不能是每排10个,因为:
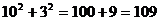 >
>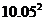 (6分)
(6分)
(3)同理: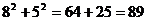 <
<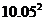
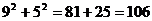 >
>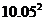
∴可以在矩形EFGH的上面和下面分别再排下8个小正方形那么现在小正方形已有了5层。 (8分)
(4)再在原来的基础上,上下再加一层,共7层,新矩形的高可以看成是7,那么新加入的这两排,每排都可以是7个但不能是8个。
∵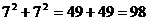 <
<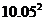
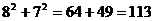 >
>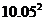 (9分)
(9分)
(5)在7层的基础上,上下再加入一层,新矩形的高可以看成是9,这两层,每排可以是4个但不能是5个。
∵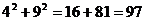 <
<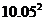
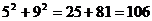 >
>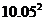
现在总共排了9层,高度达到了9,上下各剩下约0.5cm 的空间,因为矩形ABCD的位置不能调整,故再也放不下一个小正方形了。
∴10+2×9+2×8+2×7+2×4=66(个) (10分)
方法二:
学生也可能按下面的方法排列,只要说理清楚,评分标准参考方法一。
可以按9个正方形排成一排,叠4层,先放入圆内,然后:
(1)上下再加一层,每层8个,现在共有6层。
(2)在前面的基础上,上下各加6个,现在共有8层。
(3)最后上下还可加一层,但每层只能是一个,共10层。
这样共有:4×9+2×8+2×6+2×1=66(个)







 这篇博客主要围绕两部分内容展开:一是高中数学试题的解答,涉及选择题、填空题和解答题,展示了对学生解题能力的考察;二是安全疏散问题的分析,通过建立数学模型计算门的通行能力和疏散时间,确保建筑设计符合安全规定。题目涵盖了方程求解、几何相似、概率计算等多个知识点,并讨论了实际应用中的问题解决策略。
这篇博客主要围绕两部分内容展开:一是高中数学试题的解答,涉及选择题、填空题和解答题,展示了对学生解题能力的考察;二是安全疏散问题的分析,通过建立数学模型计算门的通行能力和疏散时间,确保建筑设计符合安全规定。题目涵盖了方程求解、几何相似、概率计算等多个知识点,并讨论了实际应用中的问题解决策略。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








